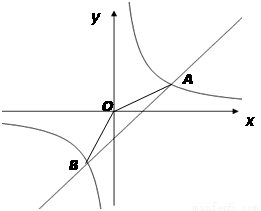
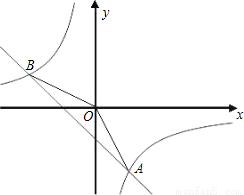
一次函数y=kx+b的图象与反比例函数y=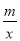 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.
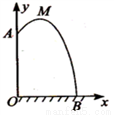
如图所示, 有一建筑工地从10m 高的窗A处用水管向外喷水,喷出的水呈抛物线状,如果抛物线的最高点M 离墙1m,离地面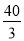 m.
m.
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.
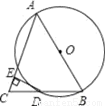
如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0).
求这条抛物线所对应的二次函数的解析式;
(2)写出它的对称轴和顶点坐标.
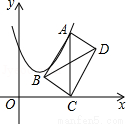
查看答案如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为____.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
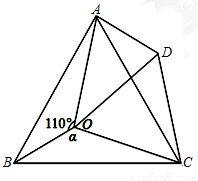
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
一次函数y=kx+b的图象与反比例函数y=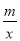 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

如图所示, 有一建筑工地从10m 高的窗A处用水管向外喷水,喷出的水呈抛物线状,如果抛物线的最高点M 离墙1m,离地面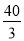 m.
m.
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.

如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.

商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0).
求这条抛物线所对应的二次函数的解析式;
(2)写出它的对称轴和顶点坐标.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知一次函数y= kx+b的图象与反比例函数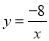 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

一次函数y=kx+b的图象与反比例函数y=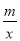 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

如图所示, 有一建筑工地从10m 高的窗A处用水管向外喷水,喷出的水呈抛物线状,如果抛物线的最高点M 离墙1m,离地面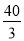 m.
m.
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.

如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.

商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
点P(-2, 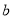 )是反比例函数
)是反比例函数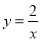 的图象上的一点,则
的图象上的一点,则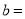 ( )
( )
A. 2 B. 1 C. -2 D. -1
D 【解析】把点P(-2, )代入反比例函数,有b==-1,所以选D.已知一次函数y= kx+b的图象与反比例函数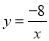 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.

如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

一次函数y=kx+b的图象与反比例函数y=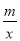 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

如图所示, 有一建筑工地从10m 高的窗A处用水管向外喷水,喷出的水呈抛物线状,如果抛物线的最高点M 离墙1m,离地面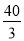 m.
m.
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.

如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 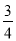 B.
B. 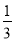 C.
C. 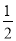 D.
D. 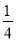
点P(-2, 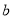 )是反比例函数
)是反比例函数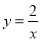 的图象上的一点,则
的图象上的一点,则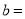 ( )
( )
A. 2 B. 1 C. -2 D. -1
查看答案已知一次函数y= kx+b的图象与反比例函数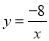 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.

如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

一次函数y=kx+b的图象与反比例函数y=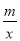 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

如图所示, 有一建筑工地从10m 高的窗A处用水管向外喷水,喷出的水呈抛物线状,如果抛物线的最高点M 离墙1m,离地面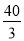 m.
m.
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列各组线段(单位:cm)中,成比例线段的是 ( )
A. 1、2、3、4 B. 1、2、2、4 C. 3、5、9、13 D. 1、2、2、3
B 【解析】选项B中1:2=2:4,所以选B.准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 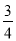 B.
B. 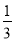 C.
C. 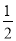 D.
D. 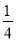
点P(-2, 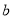 )是反比例函数
)是反比例函数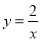 的图象上的一点,则
的图象上的一点,则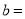 ( )
( )
A. 2 B. 1 C. -2 D. -1
查看答案已知一次函数y= kx+b的图象与反比例函数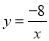 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.

如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

一次函数y=kx+b的图象与反比例函数y=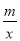 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
关于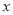 的一元二次方程
的一元二次方程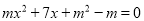 的常数项为0,则
的常数项为0,则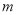 的值等于( )
的值等于( )
A. 1 B. 2 C. 0或1 D. 0
A 【解析】由题意得,m解得m=0(舍去),m=1,所以选A.下列各组线段(单位:cm)中,成比例线段的是 ( )
A. 1、2、3、4 B. 1、2、2、4 C. 3、5、9、13 D. 1、2、2、3
查看答案准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 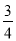 B.
B. 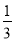 C.
C. 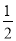 D.
D. 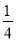
点P(-2, 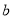 )是反比例函数
)是反比例函数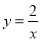 的图象上的一点,则
的图象上的一点,则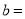 ( )
( )
A. 2 B. 1 C. -2 D. -1
查看答案已知一次函数y= kx+b的图象与反比例函数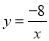 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.

如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
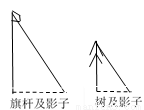
A. 4米 B. 2米 C. 1.8米 D. 3.6米
B 【解析】设旗杆的影子长x,由题意知两个图形相似,所以,解得x=2米,所以选B.关于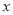 的一元二次方程
的一元二次方程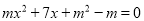 的常数项为0,则
的常数项为0,则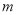 的值等于( )
的值等于( )
A. 1 B. 2 C. 0或1 D. 0
查看答案下列各组线段(单位:cm)中,成比例线段的是 ( )
A. 1、2、3、4 B. 1、2、2、4 C. 3、5、9、13 D. 1、2、2、3
查看答案准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 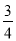 B.
B. 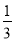 C.
C. 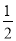 D.
D. 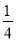
点P(-2, 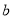 )是反比例函数
)是反比例函数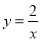 的图象上的一点,则
的图象上的一点,则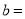 ( )
( )
A. 2 B. 1 C. -2 D. -1
查看答案已知一次函数y= kx+b的图象与反比例函数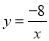 的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
的图象相交于A,B两点, 其中A点的横坐标与B点的纵坐标都是2,如图:
(1)求这个一次函数的解析式;
(2)在y轴是否存在一点P使△OAP为等腰三角形?若存在,请求出符合条件的点P坐标;若不存在,请说明理由.

- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
以下判定正确的是( )
A. 若AB⊥BC,则 ABCD是菱形 B. 若AC⊥BD,则
ABCD是菱形 B. 若AC⊥BD,则 ABCD是正方形
ABCD是正方形
C. 若AC=BD,则  ABCD是矩形 D. 若AB=AD,则
ABCD是矩形 D. 若AB=AD,则 ABCD是正方形
ABCD是正方形
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )

A. 4米 B. 2米 C. 1.8米 D. 3.6米
查看答案关于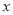 的一元二次方程
的一元二次方程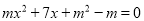 的常数项为0,则
的常数项为0,则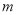 的值等于( )
的值等于( )
A. 1 B. 2 C. 0或1 D. 0
查看答案下列各组线段(单位:cm)中,成比例线段的是 ( )
A. 1、2、3、4 B. 1、2、2、4 C. 3、5、9、13 D. 1、2、2、3
查看答案准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 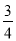 B.
B. 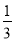 C.
C. 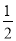 D.
D. 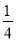
点P(-2, 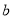 )是反比例函数
)是反比例函数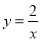 的图象上的一点,则
的图象上的一点,则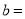 ( )
( )
A. 2 B. 1 C. -2 D. -1
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是( )
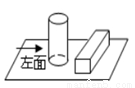
A. 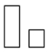 B.
B. 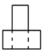 C.
C. 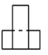 D.
D. 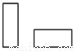
以下判定正确的是( )
A. 若AB⊥BC,则 ABCD是菱形 B. 若AC⊥BD,则
ABCD是菱形 B. 若AC⊥BD,则 ABCD是正方形
ABCD是正方形
C. 若AC=BD,则  ABCD是矩形 D. 若AB=AD,则
ABCD是矩形 D. 若AB=AD,则 ABCD是正方形
ABCD是正方形
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )

A. 4米 B. 2米 C. 1.8米 D. 3.6米
查看答案关于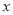 的一元二次方程
的一元二次方程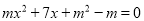 的常数项为0,则
的常数项为0,则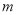 的值等于( )
的值等于( )
A. 1 B. 2 C. 0或1 D. 0
查看答案下列各组线段(单位:cm)中,成比例线段的是 ( )
A. 1、2、3、4 B. 1、2、2、4 C. 3、5、9、13 D. 1、2、2、3
查看答案准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. 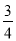 B.
B. 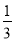 C.
C. 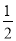 D.
D. 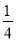
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧