0 318874 318882 318888 318892 318898 318900 318904 318910 318912 318918 318924 318928 318930 318934 318940 318942 318948 318952 318954 318958 318960 318964 318966 318968 318969 318970 318972 318973 318974 318976 318978 318982 318984 318988 318990 318994 319000 319002 319008 319012 319014 319018 319024 319030 319032 319038 319042 319044 319050 319054 319060 319068 366461
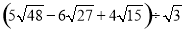 ;(2)
;(2)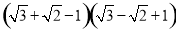
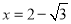 ,求代数式
,求代数式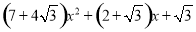 的值;
的值;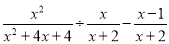 ,其中
,其中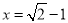
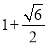 ,x2=
,x2=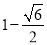 .
.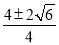 ,
, x1=
x1=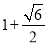 ,x2=
,x2=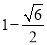 .
.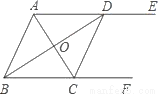
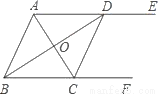
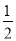 (∠DAB+∠ABC)=
(∠DAB+∠ABC)=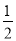 ×180°=90°,得到答案∠AOD=90°;
×180°=90°,得到答案∠AOD=90°;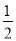 (∠DAB+∠ABC)=
(∠DAB+∠ABC)=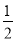 ×180°=90°,∴∠AOD=90°;
×180°=90°,∴∠AOD=90°;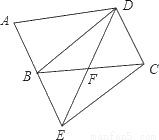
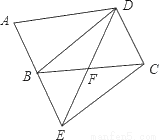
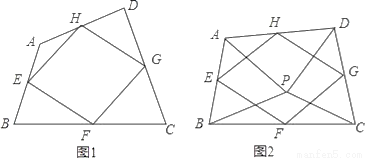
 =0 B. 2x﹣3y+1=0 C. (x﹣3)(x﹣2)=x2 D. (3x﹣1)(3x+1)=3
=0 B. 2x﹣3y+1=0 C. (x﹣3)(x﹣2)=x2 D. (3x﹣1)(3x+1)=3