小明爸爸经营的水果店出售一种优质热带水果，正在上初三的小明经过调查和计算，发现这种水果每月的销售量y(千克)与销售单价x（元）之间存在着一次函数关系：y=-10x+500(20≤x≤50)．下面是他们的一次对话：

小明：“您要是告诉我咱家这种水果的进价是多少？我就能帮你预测好多信息呢！”

爸爸：“咱家这种水果的进价是每千克20元”

聪明的你，也来解答一下小明想要解决的两个问题：

（1）若每月获得利润w(元）是销售单价x（元）的函数，求这个函数的表达式．

（2）当销售单价为多少元时，每月可获得最大利润？

如图，为了测量某电线杆（底部可到达）的高度，准备了如下的测量工具：

①平面镜；②皮尺；③长为2米的标杆；④高为1.5m的测角仪（测量仰角、俯角的仪器），请根据你所设计的测量方案，回答下列问题：

（1）画出你的测量方案示意图，并根据你的测量方案写出你所选用的测量工具；

（2）结合你的示意图，写出求电线杆高度的思路．

有这样一个问题：探究函数的图象与性质．

小东根据学习函数的经验，对函数的图象与性质进行了探究．

下面是小东的探究过程，请补充完整：

（1） 函数的自变量x的取值范围是___________；

（2）下表是y与x的几组对应值．

求m的值；

（3） 如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是(2，3)，结合函数的图象，写出该函数的其它性质（一条即可）：

在平面直角坐标系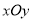中，抛物线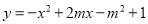的对称轴是直线．

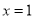（1）求抛物线的表达式；

（2）点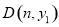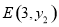， 在抛物线上，若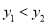，请直接写出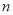的取值范围；

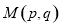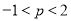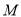（3）设点为抛物线上的一个动点，当时，点关于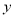轴的对称点都在直线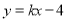的上方，求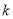的取值范围．

已知：如图，在四边形ABCD中， ，∠BCD=60º，∠ADC=45º， CA平分∠BCD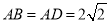， ，求四边形ABCD的面积.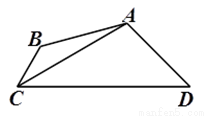

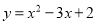对于二次函数和一次函数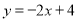，把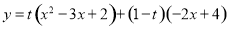称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线E. 现有点A（2，0）和抛物线E上的点B（－1，n），

请完成下列任务：

【尝试】

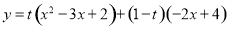（1）当t=2时，抛物线的顶点坐标为 ；

（2）点A （填在或不在）抛物线E上；

（3）n的值为 .

【发现】

通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线E总过定点，坐标为 .

【应用】

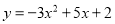二次函数是二次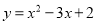函数和一次函数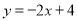的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由.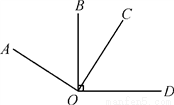

下列语句中，不是命题的是( )

A. 两点之间线段最短 B. 连接A，B两点

C. 平行于同一直线的两直线平行 D. 相等的角都是直角

如图，OB⊥OD，OC⊥OA，∠BOC＝32°，那么∠AOD等于( )

A. 148° B. 132° C. 128° D. 90°

如图，给出下列四个条件：①AC=BD；②∠DAC=∠BCA；③∠ABD=∠CDB；④∠ADB=∠CBD，其中能使AD∥BC的条件是（ ）

A. ①② B. ③④ C. ②④ D. ①③④

下列运算中，正确的是( )

A. ＝24 B. ＝3

C. ＝±9 D. －＝－