若a，b互为相反数，c，d互为倒数，且m的绝对值为2，则的值是

1. A.
   9
2. B.
   5
3. C.
   9或5
4. D.
   -7

-2的相反数是________，-（+2）是________相反数．

如图，在△ABC中，AB=8，BC=6，AC=10，D为边AC上一动点，DE⊥AB于点E，DF⊥BC于点F，则EF的最小值为

1. A.
   2.4
2. B.
   3
3. C.
   4.8
4. D.
   5

阅读以下材料并填空．
平面上有n个点（n≥2），且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
试探究以下问题：平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
（1）分析：当仅有两个点时，可连成1条直线；当仅有3个点时，可作______条直线；当有4个点时，可作______条直线；当有5个点时，可作______条直线；
（2）归纳：考察点的个数n和可作出的直线的条数Sn，发现：（填下表）

点的个数	可连成直线的条数
2
3
4
5
…
n

（3）推理：______；
（4）结论：______．

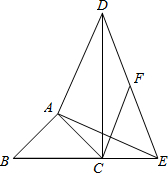已知：如图，在△ABC中，∠BAC=90°，AB=AC，点E在边BC的延长线上，DA⊥AE，AD=AE．
（1）求证：△ABE≌△ACD；
（2）如果点F是DE的中点，求证：CF=DF．

如图，一次函数y₁=kx+b的图象与反比例函数y₂=的图象相交于点A（2，3）和点B（6，1），当y₁＞y₂时，x应满足什么条件________．

当x是何值时，3x²+4x-8的值和2x²-1的值相等？

如图，它是一个人工滑雪场的框架图，其中AB=200m，AC⊥BC．一名滑雪运动员沿着斜坡，从A滑至B．当这名滑雪运动员滑行至AB的中点D处时，支架CD的长是________m．

已知抛物线y=ax²+2x+3（a≠0）有如下两个特点：①无论实数a怎样变化，其顶点都在某一条直线l上；②若把顶点的横坐标减少，纵坐标增大分别作为点A的横、纵坐标；把顶点的横坐标增加，纵坐标增加分别作为点B的横、纵坐标，则A，B两点也在抛物线y=ax²+2x+3（a≠0）上．
（1）求出当实数a变化时，抛物线y=ax²+2x+3（a≠0）的顶点所在直线l的解析式；
（2）请找出在直线l上但不是该抛物线顶点的所有点，并说明理由；
（3）你能根据特点②的启示，对一般二次函数y=ax²+bx+c（a≠0）提出一个猜想吗？请用数学语言把你的猜想表达出来，并给予证明．

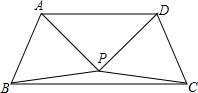如图，△APB与△CDP是两个全等的等边三角形，且PA⊥PD，有下列四个结论：①∠PBC=15°；②AD∥BC；③直线PC与AB垂直．其中正确的有

1. A.
   0个
2. B.
   1个
3. C.
   2个
4. D.
   3个