Question

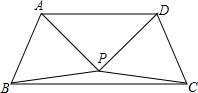如图，△APB与△CDP是两个全等的等边三角形，且PA⊥PD，有下列四个结论：①∠PBC=15°；②AD∥BC；③直线PC与AB垂直．其中正确的有

1. A.
   0个
2. B.
   1个
3. C.
   2个
4. D.
   3个

Answer 1

D
分析：根据全等三角形对应边相等可得BP=CP，AP=DP，根据等边三角形的每一个角都是60°可得∠ABP=∠APB=∠BAC=∠CPD=60°，然后利用周角等于360°求出∠BPC=150°，然后根据等腰三角形两底角相等求出∠PBC=15°；再根据等腰直角三角形的性质可得∠PAD=45°，再根据同旁内角互补求出AD∥BC；再求出∠ABC+∠PCB=90°，然后判断出PC与AB垂直．
解答：∵△APB与△CDP是两个全等的等边三角形，
∴BP=CP，AP=DP，∠ABP=∠APB=∠BAC=∠CPD=60°，
∵PA⊥PD，
∴∠BPC=360°-90°-60°×2=150°，
∴∠PBC=∠PCB=15°，故①正确；
∵PA⊥PD，
∴△APD是等腰直角三角形，
∴∠PAD=45°，
∴∠BAD+∠ABC=45°+60°+60°+15°=180°，
∴AD∥BC，故②正确；
∵∠ABC+∠PCB=60°+15°+15°=90°，
∴直线PC与AB垂直，故③正确；
综上所述，正确的有①②③共3个．
故选D．
点评：本题考查了等边三角形的性质，全等三角形的性质，等腰直角三角形的判定与性质，等腰三角形的性质，熟记各性质是解题的关键．