2.下列各式中,不能由a-b+c通过变形得到的是( )
| A. | a-(b-c) | B. | c-(b-a) | C. | (a-b)+c | D. | a-(b+c) |
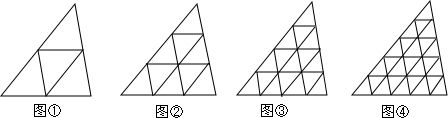
1.如图①,我们知道顺次连接三角形的三边中的(把三边二等分,此时等分数为2)可以吧原三角形分成4分形状与大小相同的小三角形,如果把三条边分别3等分(此时等分数为3),按图②方式将等分点连起来,可以看到整个三角形被分成了9个形状与大小相同的小三角形,…我们来研究这些形状与大小相同的小三角形个数a、顶点数b、边数c与等分数n之间的关系.
(1)如果把三角形的各边分别4等分、5等分,并按上述的方法连接(如图③、图④所示),请将图③、图④中的小三角形个数,顶点数,边数填入上述表格中;
(2)观察上述,如果把三角形的各边分别n等分(此时等分数为n),并按上述的方法连接,形状与大小相同的小三角形个数a,顶点数b,边数c都与等分数n存在一定的关系,请用含n的代数式分别表示出来;
(3)当n=10时,分别求出小三角形个数a、顶点数b、边数c的值.
| 等分数n | 小三角形个数a | 顶点数b | 边数c |
| 2 | 4 | 6 | 9 |
| 3 | 9 | 10 | 18 |
| 4 | 16 | 15 | 30 |
| 5 | 25 | 21 | 45 |
| … | … | … | … |
(2)观察上述,如果把三角形的各边分别n等分(此时等分数为n),并按上述的方法连接,形状与大小相同的小三角形个数a,顶点数b,边数c都与等分数n存在一定的关系,请用含n的代数式分别表示出来;
(3)当n=10时,分别求出小三角形个数a、顶点数b、边数c的值.

13.-(-a+b-1)去括号结果正确的是( )
0 311675 311683 311689 311693 311699 311701 311705 311711 311713 311719 311725 311729 311731 311735 311741 311743 311749 311753 311755 311759 311761 311765 311767 311769 311770 311771 311773 311774 311775 311777 311779 311783 311785 311789 311791 311795 311801 311803 311809 311813 311815 311819 311825 311831 311833 311839 311843 311845 311851 311855 311861 311869 366461
| A. | -a+b-1 | B. | a-b+1 | C. | -a+b+1 | D. | a+b+1 |
