题目内容
16．用代数式表示“m与n和的平方”：（m+n）2．分析 根据题意即可列出相应的代数式，从而解答本题．
解答 解：m与n和的平方为：（m+n）2
故答案为：（m+n）2．
点评 本题考查列代数的知识，关键是看清题中的信息，不要把题意理解为m与n平方的和，造成解答错误．
练习册系列答案
相关题目
6．单项式-2x3y2的系数是（ ）
| A． | 3 | B． | 2 | C． | -2 | D． | 5 |
如图，四边形ABCD中，AD∥BC，∠B=90°，AB=AD=4cm，BC=7cm，现要在形如四边形ABCD的纸片上剪下一个腰长为3cm的等腰三角形（要求：等腰三角形的一个顶点与四边形ABCD的一个顶点重合，其余两个顶点在四边形ABCD的边上），则剪下的等腰三角形的底边的长度的值有4种可能．
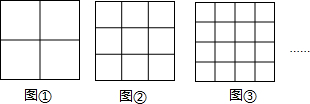
4．如图，如果在正方形中画1条纵线和1条横线，便把正方形分成4部分（如图①）；如果在正方形中画2条纵线和2条横线，便把正方形分成9部分（如图②）；如果在正方形中画3条纵线和3条横线，便把正方形分成16部分（如图③）；…，如果在正方形中画9条纵线和9条横线，便把正方形分成（ ）部分．
| A． | 72 | B． | 81 | C． | 100 | D． | 121 |
如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，∠B=40°，∠E=30°，求∠BAC的度数．
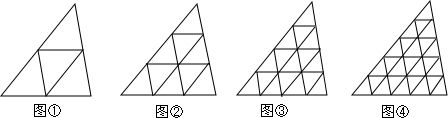
1．如图①，我们知道顺次连接三角形的三边中的（把三边二等分，此时等分数为2）可以吧原三角形分成4分形状与大小相同的小三角形，如果把三条边分别3等分（此时等分数为3），按图②方式将等分点连起来，可以看到整个三角形被分成了9个形状与大小相同的小三角形，…我们来研究这些形状与大小相同的小三角形个数a、顶点数b、边数c与等分数n之间的关系．
（1）如果把三角形的各边分别4等分、5等分，并按上述的方法连接（如图③、图④所示），请将图③、图④中的小三角形个数，顶点数，边数填入上述表格中；
（2）观察上述，如果把三角形的各边分别n等分（此时等分数为n），并按上述的方法连接，形状与大小相同的小三角形个数a，顶点数b，边数c都与等分数n存在一定的关系，请用含n的代数式分别表示出来；
（3）当n=10时，分别求出小三角形个数a、顶点数b、边数c的值．
| 等分数n | 小三角形个数a | 顶点数b | 边数c |
| 2 | 4 | 6 | 9 |
| 3 | 9 | 10 | 18 |
| 4 | 16 | 15 | 30 |
| 5 | 25 | 21 | 45 |
| … | … | … | … |
（2）观察上述，如果把三角形的各边分别n等分（此时等分数为n），并按上述的方法连接，形状与大小相同的小三角形个数a，顶点数b，边数c都与等分数n存在一定的关系，请用含n的代数式分别表示出来；
（3）当n=10时，分别求出小三角形个数a、顶点数b、边数c的值．
