16.若(1+2x)2+2|y-3|=0,则xy=( )
| A. | $\frac{1}{8}$ | B. | -1 | C. | ±1 | D. | -$\frac{1}{8}$ |
15.一动物爬行,逆时针旋转90°记为+1,则顺时针旋转180°记为( )
| A. | +3 | B. | -3 | C. | +2 | D. | -2 |
14.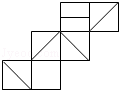 如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
0 286053 286061 286067 286071 286077 286079 286083 286089 286091 286097 286103 286107 286109 286113 286119 286121 286127 286131 286133 286137 286139 286143 286145 286147 286148 286149 286151 286152 286153 286155 286157 286161 286163 286167 286169 286173 286179 286181 286187 286191 286193 286197 286203 286209 286211 286217 286221 286223 286229 286233 286239 286247 366461
 如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
如图给定的是纸盒的外表面,下面能由它折叠而成的是( )| A. | 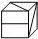 | B. | 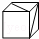 | C. |  | D. |  |
 如图所示是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和-3,折成正方体后,相对面上的两数互为相反数,则A处应填-2.
如图所示是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和-3,折成正方体后,相对面上的两数互为相反数,则A处应填-2.