19.已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值时,可以设另一个因式为x+n,则x2-4x+m=(x+3)(x+n).
即x2-4x+m=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$解得,n=-7,m=-21,
∴另一个因式为x-7,m的值为-21.
类似地,二次三项式2x2+3x-k有一个因式是2x-5,则它的另一个因式以及k的值为( )
即x2-4x+m=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$解得,n=-7,m=-21,
∴另一个因式为x-7,m的值为-21.
类似地,二次三项式2x2+3x-k有一个因式是2x-5,则它的另一个因式以及k的值为( )
| A. | x-1,5 | B. | x+4,20 | C. | x$+\frac{3}{2}$,$\frac{15}{2}$ | D. | x+4,-4 |
18. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )| A. | a-b | B. | a+b | C. | ab | D. | a2-ab |
17. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )| A. | 0<AD<3 | B. | 1≤AD<$\frac{5}{2}$ | C. | $\frac{15}{7}$≤AD<$\frac{5}{2}$ | D. | $\frac{15}{8}$≤AD<$\frac{5}{2}$ |
14. 如图,在矩形ABCD中,E是边AB上的点,将线段BE绕B点顺时针旋转一定角度后交边CD于点F,此时AE=CF,连接EF交对角线AC于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E是边AB上的点,将线段BE绕B点顺时针旋转一定角度后交边CD于点F,此时AE=CF,连接EF交对角线AC于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
0 280426 280434 280440 280444 280450 280452 280456 280462 280464 280470 280476 280480 280482 280486 280492 280494 280500 280504 280506 280510 280512 280516 280518 280520 280521 280522 280524 280525 280526 280528 280530 280534 280536 280540 280542 280546 280552 280554 280560 280564 280566 280570 280576 280582 280584 280590 280594 280596 280602 280606 280612 280620 366461
 如图,在矩形ABCD中,E是边AB上的点,将线段BE绕B点顺时针旋转一定角度后交边CD于点F,此时AE=CF,连接EF交对角线AC于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E是边AB上的点,将线段BE绕B点顺时针旋转一定角度后交边CD于点F,此时AE=CF,连接EF交对角线AC于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 6 | C. | 4$\sqrt{3}$ | D. | 8 |
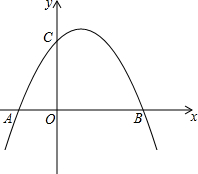 如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.
如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C. 如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动;同时一动点Q从点D出发,以每秒3个单位长度的速度沿DO向点O运动,运动到点O停止,点Q与点P同时停止.
如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动;同时一动点Q从点D出发,以每秒3个单位长度的速度沿DO向点O运动,运动到点O停止,点Q与点P同时停止.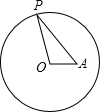 如图,点A在半径为3的⊙O内,OA=$\sqrt{3}$,P为⊙O上一点,当∠OPA取最大值时,PA的长等于$\sqrt{6}$.
如图,点A在半径为3的⊙O内,OA=$\sqrt{3}$,P为⊙O上一点,当∠OPA取最大值时,PA的长等于$\sqrt{6}$. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且$\widehat{AB}$=60°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G,H两点.若⊙O的半径为6,则GE+FH的最大值为9.