7. 小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
探究:函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质.
小东根据学习函数的经验,对函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质进行了如下探究:下面是小东的探究过程,请补充完成:
(1)函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
则m的值是$\frac{29}{6}$;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)小东进一步探究发现,该函数图象在第一象限内的最低点的坐标是$(2,\frac{3}{2})$,结合函数的图象,
写出该函数的其他性质(一条即可):当x<1时,y随x的增大而减小.
 小东同学在学习了二次函数图象以后,自己提出了这样一个问题:
小东同学在学习了二次函数图象以后,自己提出了这样一个问题:探究:函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质.
小东根据学习函数的经验,对函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的图象与性质进行了如下探究:下面是小东的探究过程,请补充完成:
(1)函数$y=\frac{1}{2}{(x-1)^2}+\frac{1}{x-1}$的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | 4 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | $-\frac{1}{2}$ | $-\frac{15}{8}$ | $-\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)小东进一步探究发现,该函数图象在第一象限内的最低点的坐标是$(2,\frac{3}{2})$,结合函数的图象,
写出该函数的其他性质(一条即可):当x<1时,y随x的增大而减小.
5. 已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
0 280090 280098 280104 280108 280114 280116 280120 280126 280128 280134 280140 280144 280146 280150 280156 280158 280164 280168 280170 280174 280176 280180 280182 280184 280185 280186 280188 280189 280190 280192 280194 280198 280200 280204 280206 280210 280216 280218 280224 280228 280230 280234 280240 280246 280248 280254 280258 280260 280266 280270 280276 280284 366461
 已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明. 
 已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}BC$,点M是边BC的中点$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$
已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}BC$,点M是边BC的中点$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$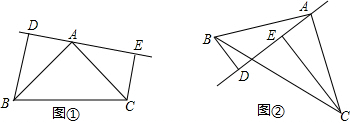


 如图,四边形ABCD中,AB∥CD,点E是边AD上的点,BE平分∠ABC,CE平分∠BCD,有下列结论:①AD=AB+CD,②E为AD的中点,③BC=AB+CD,④BE⊥CE,其中正确的有②③④.(填序号)
如图,四边形ABCD中,AB∥CD,点E是边AD上的点,BE平分∠ABC,CE平分∠BCD,有下列结论:①AD=AB+CD,②E为AD的中点,③BC=AB+CD,④BE⊥CE,其中正确的有②③④.(填序号) 如图,AE=AF,AB=AC,∠A=60°,∠B=24°,则∠AEC=96°.
如图,AE=AF,AB=AC,∠A=60°,∠B=24°,则∠AEC=96°. (1)操作发现 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.