课本P152有段文字:把函数y=2x的图像分别沿y轴向上或向下平移3个单位长度,就得到函数y=2x+3或y=2x-3的图像.
【阅读理解】
小尧阅读这段文字后有个疑问:把函数y=-2x的图像沿x轴向右平移3个单位长度,如何求平移后的函数表达式?
老师给了以下提示:如图1,在函数y=-2x的图像上任意取
两个点A、B,分别向右平移3个单位长度,得到A′、B′,
直线A′B′就是函数y=-2x的图像沿x轴向右平移3个单位长度后得到的图像.
请你帮助小尧解决他的困难.
(1)将函数y=-2x的图像沿x轴向右平移3个单位长度,平移后的函数表达式为( ▲ )
A.y=-2x+3 | B.y=-2x-3 | C.y=-2x+6 | D.y=-2x-6 |
【解决问题】
(2)已知一次函数的图像与直线y=-2x关于x轴对称,求此一次函数的表达式.

【拓展探究】
(3)一次函数y=-2x的图像绕点(2,3)逆时针方向旋转90°后得到的图像对应的函数表达式为________________.(直接写结果)
如图1所示,在A,B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图像.
 |
(1)填空:货车的速度是 _________千米/小时;
(2)求E点坐标,并说明点E的实际意义.

某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
| 甲种客车 | 乙种客车 | |
| 载客量(座/辆) | 60 | 45 |
| 租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
 图像上的点,则
图像上的点,则  B.
B. C
C .
. D.
D.
 B.
B. C.
C. D.
D.
 .5,2,2.5 C.2,3,4 D.1,
.5,2,2.5 C.2,3,4 D.1, ,3
,3 C.0 D.
C.0 D.




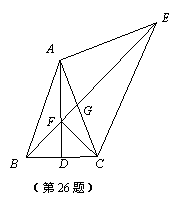 (3)求证:EF2+BF2=2AC2.
(3)求证:EF2+BF2=2AC2.