Question

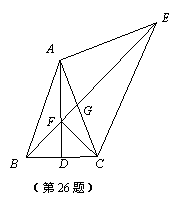
在△ABC中，AB=AC， D是BC的中点，以AC为腰向外作等腰直角△ACE，∠EAC＝90°，连接BE，交AD于点F，交AC于点G．

（1）若∠BAC＝40°，求∠AEB的度数；

（2）求证：∠AEB＝∠ACF；

（3）求证：EF²＋BF²＝2AC²．

 

Answer 1

（1）解： ∵AB＝AC，△ACE是等腰直角三角形，

∴AB＝AE．∴∠ABE＝∠AEB．…………………………………………………………… 1分

又∵∠BAC＝40°，∠EAC＝90°，

∴∠BAE＝40°＋90°＝130°…………………………………………………………… 2分，

∴∠AEB＝（180°－130°）÷2＝25°…………………………………………………………3分

（2）证明：

∵AB＝AC， D是BC的中点，∴∠BAF＝∠CAF．

在△BAF和△CAF中， ∴△BAF≌△CAF（SAS）．

∴∠ABF＝∠ACF．………………………………………………………………………… 5分

∵∠ABE＝∠AEB，∴∠AEB＝∠ACF．…………………………………………………… 6分

（3）∵△BAF≌△CAF，∴BF＝CF．

∴∠AEB＝∠ACF，∠AGE＝∠FGC．∴∠CFG＝∠EAG＝90°．………………… 7分

∴EF²＋BF²＝EF²＋CF²＝EC²．…………………………………………………………… 8分

∵△ACE是等腰直角三角形，∴∠CAE＝90°，AC＝AE．

∴EC²＝AC ²＋AE ²＝2AC²．…………………………………………………………… 9分

即EF²＋BF²＝2AC²．…………………………………………………………………………10