0 265907 265915 265921 265925 265931 265933 265937 265943 265945 265951 265957 265961 265963 265967 265973 265975 265981 265985 265987 265991 265993 265997 265999 266001 266002 266003 266005 266006 266007 266009 266011 266015 266017 266021 266023 266027 266033 266035 266041 266045 266047 266051 266057 266063 266065 266071 266075 266077 266083 266087 266093 266101 366461



 B、
B、
 D、
D、
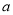 -1)x
-1)x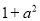 =1是一元二次方程,则
=1是一元二次方程,则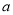 的值是( )
的值是( ) )(x+
)(x+ )+(2x-1)2=0化为一元二次方程的一般形式是( )
)+(2x-1)2=0化为一元二次方程的一般形式是( )

 gt2(g为正常数,t为时间), 则如图中函数的图像为( )
gt2(g为正常数,t为时间), 则如图中函数的图像为( )