Question

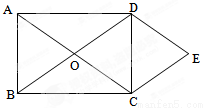
如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．

（1）旋转中心是点 ，旋转角度是 度；

（2）若连结EF，则△AEF是 三角形；并证明

Answer 1

（1）A；90；（2）△AEF是等腰直角三角形，

【解析】

试题分析：（1）利用旋转的定义直接填写即可；

（2）可证明△ADE≌△ABF，可得出AE=AF，且可求得∠EAF=90°；

试题解析：（1）由旋转的定义可知旋转中心为A，AD从AD到AB，可知旋转了90°．

（2）△AEF是等腰直角三角形，

理由如下：

∵四边形ABCD是正方形，

∴∠DAB=90°，

∵△ADE经顺时针旋转后与△ABF重合，

∴△ADE≌△ABF，∠DAB=∠EAF=90°，

∴AE=AF，

∴△AEF是等腰直角三角形；

考点：1.旋转的性质；2.点与圆的位置关系；3.作图—复杂作图．