一次函数的实际应用
| 建模思想 | 确定实际问题中的一次函数解析式,要先将实际问题转化为数学问题,即数学建模.要做到这种转化,首先要分清哪个量是自变量,哪个量是函数;其次建立 |
| 实际问题中一次函数的性质 | 在实际问题中,可以根据自变量的取值求 |
确定一次函数的解析式
| 常用方法 |
|
| 步骤 | ①设函数 |
| 常见类型 | ①已知两点坐标确定解析式;②已知两对函数对应值确定解析式;③通过平移规律确定函数解析式. |
【易错提示】在已知自变量和函数的取值范围确定函数解析式时,要注意函数性质的影响,防止漏解.
考点5 一次函数与方程、不等式的关系
| 一次函数与一次方程 | 一元一次方程kx+b=0的根就是一次函数y=kx+b(k、b是常数,k≠0)的图象与 |
| 一次函数与一元一次不等式 | 一元一次不等式kx+b>0(或kx+b<0)(k≠0)的解集可以看作一次函数y=kx+b取 |
| 一次函数与方程组 | 两直线的交点坐标是两个一次函数解析式y=k1x+b1和y=k2x+b2所组成的关于x、y的方程组 |
一次函数y=kx+b的性质
| k、b符号 | 图象形状 | 经过的象限 | 函数的性质 |
| k>0,b>0 |
|
⑭ | y随x的增大而⑯ . |
| k>0,b<0 |
|
⑮ | |
| k<0,b>0 |
|
| y随x的增大而 |
| k<0,b<0 |
|
|
一次函数的图象
| 一次函数的图象 | 一次函数y=kx+b的图象是经过点(0,④ )和(⑤ ,0)的一条⑥ . 特别地,正比例函数y=kx的图象是经过点(0,⑦ )和(1,⑧ )的一条⑨ . |
| 直线y=kx+b与y=kx之间的关系 | 直线y=kx+b可以看成是由直线y=kx平移得到,b>0,向⑩ 平移⑪ 个单位;b<0,向⑫ 平移⑬ 个单位. |
一次函数与正比例函数的概念
| 一次函数 | 一般地,如果① (k、b是常数,k≠0),那么y叫做x的一次函数. |
| 正比例函数 | 特别地,当② 时,y=kx+b变为③ (k是常数,k≠0),这时y叫做x的正比例函数. |
 与
与 之间的关系,要注意
之间的关系,要注意
 .
. ,或者由
,或者由 求自变量的值.由于自变量的取值范围一般受到限制,所以可以根据一次函数的性质求出函数在某个范围的最值.
求自变量的值.由于自变量的取值范围一般受到限制,所以可以根据一次函数的性质求出函数在某个范围的最值.
 ;②列方程(组);③解方程(组)确定待定系数;④确定解析式.
;②列方程(组);③解方程(组)确定待定系数;④确定解析式. 轴交点的
轴交点的 坐标.
坐标. 值(或
值(或 值)时自变量x的取值范围.
值)时自变量x的取值范围. 的解.
的解.



 .
.


 的运算结果= (用含字母x和n的代数式表示).
的运算结果= (用含字母x和n的代数式表示). +
+ 有意义的自变量x的取值范围是 .
有意义的自变量x的取值范围是 . 是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位……,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3整除,余数为2时,则向右走2个单位.当走完第100步时,棋子所处位置的坐标是( )
是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位……,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3整除,余数为2时,则向右走2个单位.当走完第100步时,棋子所处位置的坐标是( ) (67,33) C.(100,33) D.(99,34)
(67,33) C.(100,33) D.(99,34)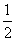 MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(2a,b+1),则a与b的数量关系为( )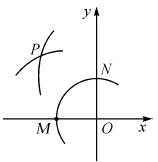
 到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )
到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )