题目内容
如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M,N为圆心，大于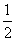
MN的长为半径画弧，两弧在第二象限交于点P，若点P的坐标为(2a,b+1)，则a与b的数量关系为( )
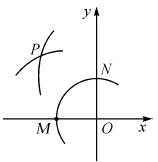
A.a=b B.2a+b=-1 C.2a-b=1 D.2a+b=1
B
的解满足x+y＞1，则k的取值范围是 .平面直角坐标系
| 定义 | 平面内，两条互相① 、原点② 的数轴组成平面直角坐标系.坐标平面内的点与③ 实数对一一对应. |
| 坐标系内点的坐标特征 | 第一象限④ ；第二象限⑤ ；第三象限⑥ ；第四象限⑦ . |
| 坐标轴上点的坐标特征 | x轴负半轴⑧ ；x轴正半轴⑨ ；y轴负半轴⑩ ；y轴正半轴⑪ ；原点⑫ . |
| 象限角平分线上点的坐标特征 | 一、三象限角平分线上的点，横坐标与纵坐标⑬ ； 二、四象限角平分线上的点，横坐标与纵坐标⑭ . |
一次函数的图象
| 一次函数的图象 | 一次函数y=kx+b的图象是经过点(0,④ )和(⑤ ,0)的一条⑥ . 特别地，正比例函数y=kx的图象是经过点(0，⑦ )和(1，⑧ )的一条⑨ . |
| 直线y=kx+b与y=kx之间的关系 | 直线y=kx+b可以看成是由直线y=kx平移得到，b＞0，向⑩ 平移⑪ 个单位；b＜0，向⑫ 平移⑬ 个单位. |
C.y=5x2+6 D.y=-0.5x-1
(k>0)刻画(如图所示).