题目内容
使函数y=
+
有意义的自变量x的取值范围是 .
x＞-2且x≠1
天天向上一本好卷系列答案
小学生10分钟应用题系列答案某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：
| A | B | |
| 进价（元/件） | 1 200 | 1 000 |
| 售价（元/件） | 1 380 | 1 200 |
（1）该商场购进A、B两种商品各多少件？
（2）商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售
．若两种商品销售完毕，要使第二次经营活动获利不少于81 600元，B种商品最低售价为每件多少元？
平移与对称点的坐标
| 点的平移 | 将点P(x，y)向右(或向左)平移a个单位，得对应点坐标为 将点P(x，y)向上(或向下)平移b个单位，得对应点坐标为 |
| 关于坐标轴对称 | 点P(x,y)关于x轴的对称点坐标为 点P(x,y)关于y轴的对称点坐标为 |
| 关于原点对称 | 点P(x, |
；
.
；
.
y)关于原点对称的点坐标为
.
，则输出的函数值为( )
B.
C.
D.
确定一次函数的解析式
| 常用方法 |
|
| 步骤 | ①设函数 |
| 常见类型 | ①已知两点坐标确定解析式；②已知两对函数对应值确定解析式；③通过平移规律确定函数解析式. |
；②列方程(组)；③解方程（组)确定待定系数；④确定解析式.【易错提示】在已知自变量和函数的取值范围确定函数解析式时，要注意函数性质的影响，防止漏解.
考点5 一次函数与方程、不等式的关系
| 一次函数与一次方程 | 一元一次方程kx+b=0的根就是一次函数y=kx+b(k、b是常数,k≠0)的图象与 |
| 一次函数与一元一次不等式 | 一元一次不等式kx+b＞0(或kx+b＜0)(k≠0)的解集可以看作一次函数y=kx+b取 |
| 一次函数与方程组 | 两直线的交点坐标是两个一次函数解析式y=k1x+b1和y=k2x+b2所组成的关于x、y的方程组 |
轴交点的
坐标.
值(或
值)时自变量x的取值范围.
的解.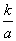
(k是常数，k≠0).已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶700千米.