C.(4，1) D.(0，1)
函数的有关概念
| 自变量与函数 | 一般地，在某个变化过程中，如果有两个变量x和y，如果对于x的每一个值，y都有 |
| 函数的表示方法 | 列表法、图象法、解析法 |
| 函数自变量的取值范围 | ①函数解析式是整式，自变量取值是 ②函数解析式是分式，自变量取值使得 ③函数解析式是偶次根式，自变量要使得 ④来源于实际问题的函数，自变量要使得实际问题有意义、式子有意义. |
| 函数的图象 | 一般地，对于一个函数，如果把自变量与函数的每对对应值分别作 |
的值与之对应，那么y是x的函数，其中x是自变量.
；
；
为非负数；
坐标、
坐标，那么坐标平面内由这些点组成的图象，就是这个函数的图象.平移与对称点的坐标
| 点的平移 | 将点P(x，y)向右(或向左)平移a个单位，得对应点坐标为 将点P(x，y)向上(或向下)平移b个单位，得对应点坐标为 |
| 关于坐标轴对称 | 点P(x,y)关于x轴的对称点坐标为 点P(x,y)关于y轴的对称点坐标为 |
| 关于原点对称 | 点P(x, |
；
.
；
.
y)关于原点对称的点坐标为
.
.平面直角坐标系
| 定义 | 平面内，两条互相① 、原点② 的数轴组成平面直角坐标系.坐标平面内的点与③ 实数对一一对应. |
| 坐标系内点的坐标特征 | 第一象限④ ；第二象限⑤ ；第三象限⑥ ；第四象限⑦ . |
| 坐标轴上点的坐标特征 | x轴负半轴⑧ ；x轴正半轴⑨ ；y轴负半轴⑩ ；y轴正半轴⑪ ；原点⑫ . |
| 象限角平分线上点的坐标特征 | 一、三象限角平分线上的点，横坐标与纵坐标⑬ ； 二、四象限角平分线上的点，横坐标与纵坐标⑭ . |
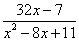的值.