题目内容
关于x的一元二次方程(a-6)x2-8x+9=0有实根.
(1)求a的最大整数值;
(2)当a取最大整数值时,①求出该方程的根;②求2x2-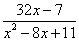 的值.
的值.
(1)∵关于x的一元二次方程(a-6)x2-8x+9=0有实根,
∴a-6≠0,Δ=(-8)2-4×(a-6)×9≥0.
解得a≤ 且a≠6.
且a≠6.
∴a的最大整数值为7.
(2)①当a=7时,原一元二次方程变为
x2-8x+9=0.
解得x1=4+ ,x2=4-
,x2=4- .
.
②∵x是一元二次方程x2-8x+9=0的根,
∴x2-8x=-9.
∴原式=2x2- =2x2-16x+
=2x2-16x+ =2(x2-8x)+
=2(x2-8x)+ =2×(-9)+
=2×(-9)+ =-
=- .
.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
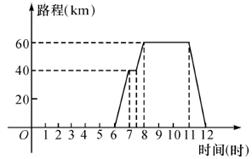
函数的有关概念
| 自变量与函数 | 一般地,在某个变化过程中,如果有两个变量x和y,如果对于x的每一个值,y都有 |
| 函数的表示方法 | 列表法、图象法、解析法 |
| 函数自变量的取值范围 | ①函数解析式是整式,自变量取值是 ②函数解析式是分式,自变量取值使得 ③函数解析式是偶次根式,自变量要使得 ④来源于实际问题的函数,自变量要使得实际问题有意义、式子有意义. |
| 函数的图象 | 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作 |
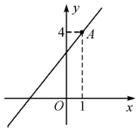
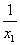 +
+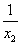 =-
=-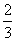 ,求a的值.
,求a的值. 的值与之对应,那么y是x的函数,其中x是自变量.
的值与之对应,那么y是x的函数,其中x是自变量. ;
; ;
; 为非负数;
为非负数; 坐标、
坐标、 坐标,那么坐标平面内由这些点组成的图象,就是这个函数的图象.
坐标,那么坐标平面内由这些点组成的图象,就是这个函数的图象. 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .