题目内容
已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0，其中a、b、c分别为△ABC的三边的长.
(1)如果x=-1是方程的根，试判断△ABC的形状，并说明理由；
(2)如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
(3)如果△ABC是等边三角形，试求这个一元二次方程的根.
(1)把x=-1代入方程得2a-2b=0，即a=b，
∴△ABC是等腰三角形.
(2)∵方程有两个相等的实数根，
∴Δ=(2b
)2-4(a+c)(a-c)=0，即b2+c2=a2，
∴△ABC是直角三角形.
(3)∵△ABC是等边三角形，∴a=b=c.
∴原方程变为：2ax2+2ax=0.
∵a≠0，∴x2+x=0.
∴x1=0，x2=-1.
练习册系列答案
相关题目
B.x>2 C.x>-2 D.x>8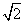
x+m=0,有两个不相等的实数根.
中,自变量x的取值范围是( )
到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )