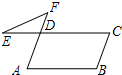
 如图,在?ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F=( )
如图,在?ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F=( )| A、110° | B、70° |
| C、50° | D、30° |
 如图,点A是半径为3的⊙O内一定点,已知OA=
如图,点A是半径为3的⊙O内一定点,已知OA=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点E、F.若AD=2,BC=6,则△ADB的面积等于( )
如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点E、F.若AD=2,BC=6,则△ADB的面积等于( )| A、2 | B、4 | C、6 | D、8 |
 如图,在?ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F=( )
如图,在?ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F=( )| A、110° | B、70° |
| C、50° | D、30° |
 如图,点A是半径为3的⊙O内一定点,已知OA=
如图,点A是半径为3的⊙O内一定点,已知OA=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点E、F.若AD=2,BC=6,则△ADB的面积等于( )
如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点E、F.若AD=2,BC=6,则△ADB的面积等于( )| A、2 | B、4 | C、6 | D、8 |