题目内容
 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)如图,当点O在△ABC内时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案,不需说明理由.)
考点:中点四边形
专题:
分析:(1)首先利用三角形中位线的性质得出DE∥BC,DE=
BC,同理,GF∥BC,GF=
BC,即可得出DE∥GF,DE=GF即可得出四边形DGFE是平行四边形;
(2)利用(1)中所求,只要邻边再相等即可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用(1)中所求,只要邻边再相等即可得出答案.
解答:(1)证明:∵D、E分别是边AB、AC的中点.
∴DE∥BC,DE=
BC.
同理,GF∥BC,GF=
BC.
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形.
(2)解:解法一:点O的位置满足两个要求:AO=BC,且点O不在射线CD、射线BE上.
∵由(1)得出四边形DEFG是平行四边形,
∴点O的位置满足两个要求:AO=BC,且点O不在射线CD、射线BE上时,
可得GD=
AO,GE=
BC,
∴DG=GE,
∴平行四边形DEFG是菱形;
解法二:点O在以A为圆心,BC为半径的一个圆上,但不包括射线CD、射线BE与⊙A的交点.
解法三:过点A作BC的平行线l,点O在以A为圆心,BC为半径的一个圆上,但不包括l与⊙A的两个交点.
∴DE∥BC,DE=
| 1 |
| 2 |
同理,GF∥BC,GF=
| 1 |
| 2 |
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形.
(2)解:解法一:点O的位置满足两个要求:AO=BC,且点O不在射线CD、射线BE上.
∵由(1)得出四边形DEFG是平行四边形,
∴点O的位置满足两个要求:AO=BC,且点O不在射线CD、射线BE上时,
可得GD=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG=GE,
∴平行四边形DEFG是菱形;
解法二:点O在以A为圆心,BC为半径的一个圆上,但不包括射线CD、射线BE与⊙A的交点.
解法三:过点A作BC的平行线l,点O在以A为圆心,BC为半径的一个圆上,但不包括l与⊙A的两个交点.
点评:此题主要考查了中点四边形的判定以及三角形的中位线的性质和平行四边形以及菱形的判定等知识,熟练掌握相关的定理是解题关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
用配方法将关于x的方程x2+5x+n=0可以变形为(x+p)2=9,那么用配方法也可以将关于x的方程x2-5x+n=-1变形为下列形式( )
| A、(x-p+1)2=10 |
| B、(x-p)2=8 |
| C、(x-p-1)2=8 |
| D、(x-p)2=10 |
 如图,四边形ABCD,∠A=130°,点D在AB、AC的垂直平分线上,则∠BDC=( )
如图,四边形ABCD,∠A=130°,点D在AB、AC的垂直平分线上,则∠BDC=( )| A、90° | B、100° |
| C、120° | D、130° |
 如图,点A是半径为3的⊙O内一定点,已知OA=
如图,点A是半径为3的⊙O内一定点,已知OA=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
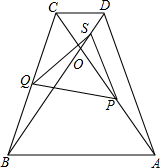 如图所示等腰梯形ABCD中,AD=BC,AB∥CD,对角线AC与BD交于O,∵∠ACD=60°,点S、P、Q分别是OD,OA,BC的中点.
如图所示等腰梯形ABCD中,AD=BC,AB∥CD,对角线AC与BD交于O,∵∠ACD=60°,点S、P、Q分别是OD,OA,BC的中点.