长方形的一条对角线的长为10cm,一边长为6cm,它的面积是( )
| A、60cm2 |
| B、64cm2 |
| C、24cm2 |
| D、48cm2 |
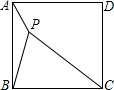 已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )
已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )| A、120? | B、125? |
| C、135? | D、150? |
| A、60cm2 |
| B、64cm2 |
| C、24cm2 |
| D、48cm2 |
 已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )
已知如图,正方形ABCD中,P是内部一点,且点P到A、B、C三点的距离分别是1、2、3,则图中∠APB的度数是( )| A、120? | B、125? |
| C、135? | D、150? |