题目内容
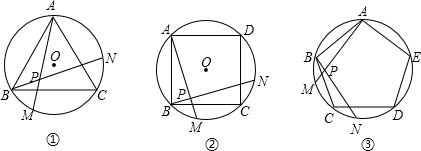
如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在⊙O上逆时针运动.
(1)求图①中∠APN的度数(写出解题过程);
(2)写出图②中∠APN的度数和图③中∠APN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
(1)求图①中∠APN的度数(写出解题过程);
(2)写出图②中∠APN的度数和图③中∠APN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)

考点:圆的综合题
专题:
分析:(1)由△ABC为等边三角形可知∠ABC=60°,再由等速运动可得到∠ABP=∠NBC,再利用外角的性质可得∠APN=∠ABP+∠BAP,代换可得到∠APN=∠ABC,可求得∠APN的度数;
(2)和(1)同理可得到∠APN的度数和∠ABC的度数相等,图③中∠APN的度数和∠ABC的度数相等;
(3)结合(1)(2)可得到∠APN的度数等于多边形的内角的度数,可得到结论.
(2)和(1)同理可得到∠APN的度数和∠ABC的度数相等,图③中∠APN的度数和∠ABC的度数相等;
(3)结合(1)(2)可得到∠APN的度数等于多边形的内角的度数,可得到结论.
解答:解:(1)∠APN=60°.
∵∠APN=∠ABP+∠BAP,
且点M、N以相同的速度中⊙O上逆时针运动,
∴
=
,
∴∠ABP=∠NBC,
∴∠APN=∠ABP+∠NBC,
即∠APN=∠ABC=60°;
(2)同理:图2中,∠APN=∠ABC=90°;图3中,∠APN=∠ABC=108°;
(3)由(1)(2)可知∠APN的度数等于多边形的内角的度数,
当正多边形为n边形时,其内角和为(n-2)180°,
所以每个内角的度数为
,
所以∠APN=
.
∵∠APN=∠ABP+∠BAP,
且点M、N以相同的速度中⊙O上逆时针运动,
∴
 |
| BM |
 |
| CN |
∴∠ABP=∠NBC,
∴∠APN=∠ABP+∠NBC,
即∠APN=∠ABC=60°;
(2)同理:图2中,∠APN=∠ABC=90°;图3中,∠APN=∠ABC=108°;
(3)由(1)(2)可知∠APN的度数等于多边形的内角的度数,
当正多边形为n边形时,其内角和为(n-2)180°,
所以每个内角的度数为
| (n-2)180° |
| n |
所以∠APN=
| (n-2)180° |
| n |
点评:本题主要考查圆周角定理及正多边形的性质,在(1)中利用弧相等得到角相等,从而得到∠APN和∠ABC的关系是解题的关键,在(3)中总结得出∠APN的度数等于多边形的内角的度数是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若n为不等式n200>3300的解,则n取最小整数的值为( )
| A、4 | B、5 | C、6 | D、7 |
长方形的一条对角线的长为10cm,一边长为6cm,它的面积是( )
| A、60cm2 |
| B、64cm2 |
| C、24cm2 |
| D、48cm2 |
