某私营服装厂根据2011年市场分析,决定2012年调整服装制作方案,准备每周(按120工时计算)制作西服、休闲服、衬衣共360件,且衬衣至少60件.已知每件服装的收入和所需工时如下表:
设每周制作西服x件,休闲服y件,衬衣z件.
(1)请你分别从件数和工时数两个方面用含有x,y的代数式表示衬衣的件数z.
(2)求y与x之间的函数关系式.
(3)问每周制作西服、休闲服、衬衣各多少件时,才能使总收入最高?最高总收入是多少?
0 158005 158013 158019 158023 158029 158031 158035 158041 158043 158049 158055 158059 158061 158065 158071 158073 158079 158083 158085 158089 158091 158095 158097 158099 158100 158101 158103 158104 158105 158107 158109 158113 158115 158119 158121 158125 158131 158133 158139 158143 158145 158149 158155 158161 158163 158169 158173 158175 158181 158185 158191 158199 366461
| 服装名称 | 西服 | 休闲服 | 衬衣 |
| 工时/件 |  |  |  |
| 收入(百元)/件 | 3 | 2 | 1 |
(1)请你分别从件数和工时数两个方面用含有x,y的代数式表示衬衣的件数z.
(2)求y与x之间的函数关系式.
(3)问每周制作西服、休闲服、衬衣各多少件时,才能使总收入最高?最高总收入是多少?
 ,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是 .
,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是 .
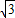 ,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2012C2012,则m= .点C2012的坐标是 .
,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2012C2012,则m= .点C2012的坐标是 .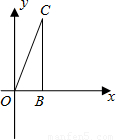
 ,再在0,-1,2中选取一个适当的数代入求值.
,再在0,-1,2中选取一个适当的数代入求值.

 CD,
CD, 的值.
的值.
 ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.