Question

已知，如图，△OBC中是直角三角形，OB与x轴正半轴重合，∠OBC=90°，且OB=1，BC=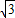，将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB₁=OC，得到△OB₁C₁，将△OB₁C₁绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB₂=OC₁，得到△OB₂C₂，…，如此继续下去，得到△OB₂₀₁₂C₂₀₁₂，则m=    ．点C₂₀₁₂的坐标是    ．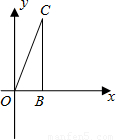

Answer 1

【答案】分析：先解直角三角形求出∠BOC=60°，再根据30°角所对的直角边等于斜边的一半即可求出m的值，然后求出OC₁、OC₂、OC₃、…、OC_n的长度，再根据周角等于360°，每6个为一个循环组，求出点C₂₀₁₂是第几个循环组的第几个点，再根据变化规律写出点的坐标即可．
解答：解：∵∠OBC=90°，OB=1，BC=，
∴tan∠BOC==，
∴∠BOC=60°，
∴OC=2OB=2×1=2，
∵将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB₁=OC，
∴m=2，
∴OC₁=2OC=2×2=4=2²，
OC₂=2OC₁=2×4=8=2³，
OC₃=2OC₂=2×8=16=2⁴，
…，
OC_n=2ⁿ⁺¹，
∴OC₂₀₁₂=2²⁰¹³，
∵2012÷6=335…2，
∴点C₂₀₁₂与点C₂x在同一射线上，在x轴负半轴，坐标为（-2²⁰¹³，0）．
故答案为：2，（-2²⁰¹³，0）．
点评：本题考查了坐标与图形的变化-旋转，解直角三角形，根据解直角三角形，以及30°角所对的直角边等于斜边的一半，求出m的值是解题的关键．