Question

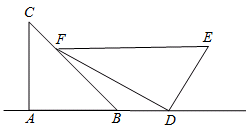
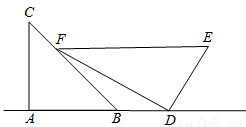
小明是一位善于思考的学生，在一次数学活动课上，他将一副直角三角板如图位置摆放，A、B、D在同一直线上，EF∥AD，∠A=∠EDF=90°，∠C=45°，∠E=60°，量得DE=8，试求BD的长．

Answer 1

【答案】分析：过点F作FM⊥AD于M，利用在直角三角形中，30°角所对的直角边等于斜边的一半和平行线的性质以及等腰直角三角形的性质即可求出BD的长．
解答：解：过点F作FM⊥AD于M，
∵∠EDF=90°，∠E=60°，
∴∠EFD=30°，
∵DE=8，
∴EF=16，
∴DF==8，
∵EF∥AD，
∴∠FDM=30°，
∴FM=DF=4，
∴MD==12，
∵∠C=45°，
∴∠MFB=∠B=45°，
∴FM=BM=4，
∴BD=DM-BM=12-4．
点评：本题考查了勾股定理的运用、平行线的性质以及等腰直角三角形的性质，解题的关键是作垂直构造直角三角形，利用勾股定理求出DM的长．