题目内容
在△ABC中,AB=AC,边BC的中点是D,作一等边△DEF,使E、F分别在边AB和AC上,问等边△DEF的边EF与BC平行吗?为什么?
考点:全等三角形的判定与性质
专题:
分析:分类讨论:(1)△ABC是锐角三角形,(2)△ABC是钝角三角形,分别画出图形,求证EF∥BC即可解题.
解答:解:(1)若∠BDE=∠CDF=60°时,EF与BC平行,

理由:AB=AC,则∠B=C,
又BD=DC,∠BDE=∠CDF=60°
∴△BDE≌△CDF,
∴DE=DF,∠EDF=60°,
∴△DEF为等边三角形,∠DEF=60°,
∴∠DEF=∠BDE=60°
∴EF与BC平行.
(2)若∠BDE≠∠CDF时,等边三角形DEF的边EF与BC不平行,此时∠A=120°,

过D作DG⊥AB于G,在BA上依次取E,H两点,使GE=GH,连结AD,
则DE=DH,∠DEG=∠DHG,过H作HF∥BC交AC于F,显然EF与BC不平行;
∵AB=AC,
∴AH=AF,
∵在△AHD和△AFD中,
,
∴△AHD≌△AFD,(SAS)
∴DF=DH=DE,∠AFD=∠AHD,
又∵∠DHG+∠AHD=180°,
∴∠DEG+∠AFD=180°,
∴∠BAC+∠EDF=180°,
∴当∠BAC=120°时,∠EDF=60°,△DEF为等边三角形
即可作出等边三角形DEF,使边EF与BC不平行,此时∠A=120°.

理由:AB=AC,则∠B=C,
又BD=DC,∠BDE=∠CDF=60°
∴△BDE≌△CDF,
∴DE=DF,∠EDF=60°,
∴△DEF为等边三角形,∠DEF=60°,
∴∠DEF=∠BDE=60°
∴EF与BC平行.
(2)若∠BDE≠∠CDF时,等边三角形DEF的边EF与BC不平行,此时∠A=120°,

过D作DG⊥AB于G,在BA上依次取E,H两点,使GE=GH,连结AD,
则DE=DH,∠DEG=∠DHG,过H作HF∥BC交AC于F,显然EF与BC不平行;
∵AB=AC,
∴AH=AF,
∵在△AHD和△AFD中,
|
∴△AHD≌△AFD,(SAS)
∴DF=DH=DE,∠AFD=∠AHD,
又∵∠DHG+∠AHD=180°,
∴∠DEG+∠AFD=180°,
∴∠BAC+∠EDF=180°,
∴当∠BAC=120°时,∠EDF=60°,△DEF为等边三角形
即可作出等边三角形DEF,使边EF与BC不平行,此时∠A=120°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AHD≌△AFD是解题的关键.

练习册系列答案
相关题目
 如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.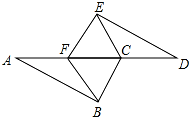 如图,已知AB∥DE,AB=DE,AF=DC,请问图中有
如图,已知AB∥DE,AB=DE,AF=DC,请问图中有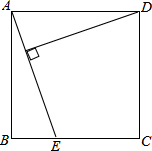 如图,正方形ABCD的面积为10cm2,在边BC上取一点E,连接AE,若AE=4cm,求点D到AE的距离.
如图,正方形ABCD的面积为10cm2,在边BC上取一点E,连接AE,若AE=4cm,求点D到AE的距离.