题目内容
 如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.考点:多边形内角与外角,三角形的外角性质
专题:
分析:连接CD,由三角形内角和外角的关系可知∠E+∠F=∠ECD+∠CDF,由四边形内角和是360°,即可求∠A+∠B+∠BCE+∠ADF+∠E+∠F=360°.
解答: 解:如图,连接CD.
解:如图,连接CD.
∵∠1=∠E+∠F,∠1=∠ECD+∠CDF,
∴∠E+∠F=∠ECD+∠CDF,
∴∠A+∠B+∠BCE+∠ADF+∠E+∠F
=∠A+∠B+∠BCE+∠ADF+∠ECD+∠CDF
=∠A+∠B+∠BCD+∠CDA.
又∵∠A+∠B+∠BCD+∠CDA=360°,
∴∠A+∠B+∠BCE+∠ADF+∠E+∠F=360°.
 解:如图,连接CD.
解:如图,连接CD.∵∠1=∠E+∠F,∠1=∠ECD+∠CDF,
∴∠E+∠F=∠ECD+∠CDF,
∴∠A+∠B+∠BCE+∠ADF+∠E+∠F
=∠A+∠B+∠BCE+∠ADF+∠ECD+∠CDF
=∠A+∠B+∠BCD+∠CDA.
又∵∠A+∠B+∠BCD+∠CDA=360°,
∴∠A+∠B+∠BCE+∠ADF+∠E+∠F=360°.
点评:本题考查的是三角形内角与外角的关系,涉及到四边形及三角形内角和定理,比较简单.

练习册系列答案
相关题目
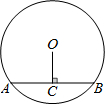 如图,已知⊙O的半径为5,点O到弦AB的距离为3,则弦AB的长为( )
如图,已知⊙O的半径为5,点O到弦AB的距离为3,则弦AB的长为( )| A、8 | B、6 | C、5 | D、4 |
 如图,求△AOB的面积.
如图,求△AOB的面积.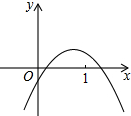 二次函数y=ax2+bx+c的图象如图所示,则下面正确的结论有( )
二次函数y=ax2+bx+c的图象如图所示,则下面正确的结论有( )