题目内容
小明在玩一副三角板时发现:含45°角的直角三角板的斜边可与含30°角的直角三角板的较长直角边完全重合(如图①).即△C´DA´的顶点A´、C´分别与△BAC的顶点A、C重合.现在,他让△C´DA´固定不动,将△BAC通过变换使斜边BC经过△C´DA´的直角顶点D.


(1)如图②,将△BAC绕点C按顺时针方向旋转角度α(0°<α<180°),使BC边经过点D,则α= °.
(2)如图③,将△BAC绕点A按逆时针方向旋转,使BC边经过点D.试说明:BC∥A´C´.
(3)如图④,若AB= ,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.
,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.


(1)如图②,将△BAC绕点C按顺时针方向旋转角度α(0°<α<180°),使BC边经过点D,则α= °.
(2)如图③,将△BAC绕点A按逆时针方向旋转,使BC边经过点D.试说明:BC∥A´C´.
(3)如图④,若AB=
 ,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.
,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.(1)15°;(2)过点A作AH⊥BC.垂足为H.根据旋转可得:旋转角∠CA C´=∠BAH.在Rt△ABC中,由AH⊥BC可得∠C=∠BAH,则∠CA C´=∠C,从而可以证得结论;(3) -
-
 -
-
试题分析:(1)根据旋转角的定义结合直角三角板的特征即可求得结果;
(2)过点A作AH⊥BC.垂足为H.根据旋转可得:旋转角∠CA C´=∠BAH.在Rt△ABC中,由AH⊥BC可得∠C=∠BAH,则∠CA C´=∠C,从而可以证得结论;
(3)过点D作DH⊥AC,垂足为H.由DH=
 A´C´=
A´C´= ,△DHC∽△BAC,根据相似三角形的性质可得CH=
,△DHC∽△BAC,根据相似三角形的性质可得CH= ,即可求得结果.
,即可求得结果.(1)如图②,α=∠A´C´A=45°-30°=15°;
(2)如图③,过点A作AH⊥BC.垂足为H.
根据旋转可得:旋转角∠CA C´=∠BAH.
在Rt△ABC中,∵AH⊥BC,
∴∠C=∠BAH
∴∠CA C´=∠C
∴BC∥A´C´;
(3)如图④,过点D作DH⊥AC,垂足为H.
由DH=
 A´C´=
A´C´= ,△DHC∽△BAC,可得CH=
,△DHC∽△BAC,可得CH= .
.所以m的值为
 -
- .
.
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目





 放置于矩形
放置于矩形 上,
上, 三角板的一个
三角板的一个 角的顶点放在
角的顶点放在 处, 且直角边
处, 且直角边 在矩形内部绕点
在矩形内部绕点 与
与 交于点
交于点 .
.  与
与 的有何数量关系?并说明理由;
的有何数量关系?并说明理由; 为等腰三角形,若存在,求出
为等腰三角形,若存在,求出 为边在矩形内部作正方形
为边在矩形内部作正方形 ,直角边
,直角边 于
于 ,交
,交 于
于 .设
.设 写出
写出 关于
关于 的函数关系式.
的函数关系式.
 中,
中,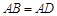 ,
,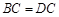 ,
,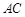 与
与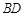 相交于点
相交于点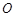 ,下列判断正确的有 .(填序号).
,下列判断正确的有 .(填序号).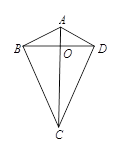
 ;
; ;
;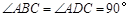 ;
;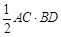 .
.
 ABCD中,
ABCD中, 为
为 边上一点,且
边上一点,且 .
.
 .
. 平分
平分 ,
, ,求
,求 的度数.
的度数.