题目内容
6. 已知如图,E、F是AB上的两点,AE=BF,AC∥BD,且AC=DB,求证:(1)CF=DE.(2)CF∥DE.
已知如图,E、F是AB上的两点,AE=BF,AC∥BD,且AC=DB,求证:(1)CF=DE.(2)CF∥DE.
分析 先由AE=BF得AF=BE和由AC∥BD得∠A=∠B,再加AC=DB,则可证明△ACF≌△BDE,则CF=DE,∠CFA=∠DEB,根据内错角相等证明两直线平行即可.
解答 证明:(1)∵AE=BF,
∴AF=BE.
∵AC∥BD,
∴∠A=∠B.
在△ACF和△BDE中,
$\left\{\begin{array}{l}{AC=DB}\\{∠A=∠B}\\{AF=BE}\end{array}\right.$,
∴△ACF≌△BDE(SAS).
∴CF=DE,
(2)∵△ACF≌△BDE,
∴∠CFA=∠DEB,
∴CF∥DE.
点评 此题考查三角形全等的判定和性质,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
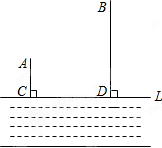 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米. 平面直角坐标系中,A(-2,0),B(-3,4),试在y轴上求作一点C,使AC+BC最短,求出点C的坐标.
平面直角坐标系中,A(-2,0),B(-3,4),试在y轴上求作一点C,使AC+BC最短,求出点C的坐标. 如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,BE=2,求弦CD的长.
如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,BE=2,求弦CD的长. 如图,已知∠1=∠2,且AB•ED=AD•BC,则△ABC与△ADE相似吗?是说明理由.
如图,已知∠1=∠2,且AB•ED=AD•BC,则△ABC与△ADE相似吗?是说明理由. 如图,AB∥DE,探究∠B、∠C、∠D、∠F的关系.
如图,AB∥DE,探究∠B、∠C、∠D、∠F的关系.