题目内容
18．
如图，在⊙O中，直径AB=10，弦CD⊥AB，垂足为E，BE=2，求弦CD的长．
分析 如图，连接OC；首先证明CE=DE；其次运用勾股定理求出CE的长，即可解决问题．
解答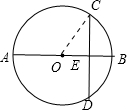 
解：如图，连接OC；
∵直径AB=10，BE=2，
∴OE=5-2=3，OC=5；
∵弦CD⊥AB，
∴CE=DE；由勾股定理得：
CE=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴CD=2CE=8．
点评 该题主要考查了勾股定理、垂径定理等几何知识点及其应用问题；解题的关键是作辅助线，灵活运用勾股定理、垂径定理等几何知识点来分析、判断、求解．
练习册系列答案
相关题目
已知如图，E、F是AB上的两点，AE=BF，AC∥BD，且AC=DB，求证：（1）CF=DE．（2）CF∥DE．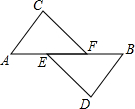
已知，AE=BF，AC∥DB，AC=DB，证明：CF=DE．
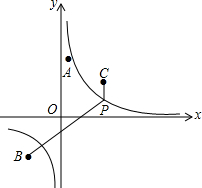如图，点A，B，C的坐标分别为（1，5），（-4，-4），（4，4），点P为双曲线y=$\frac{8}{x}$（x＞0）上一个动点．