题目内容
16.解方程(组):(1)$\frac{x+1}{2}$-2=$\frac{2-3x}{3}$;
(2)$\left\{\begin{array}{l}{2+3y=-1}\\{3x-2y=8}\end{array}\right.$.
分析 (1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(2)方程组中第一个方程求出y的值,代入第二个方程求出x的值即可.
解答 解:(1)去分母得:3x+3-12=4-6x,
移项合并得:9x=13,
解得:x=$\frac{13}{9}$;
(2)$\left\{\begin{array}{l}{2+3y=-1①}\\{3x-2y=8②}\end{array}\right.$,
由①得:y=-1,
把y=-1代入②得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
7.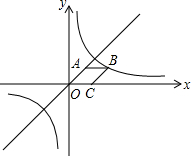 如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )
如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )
 如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )
如图,点C在x轴的正半轴上,菱形OCBA的面积为$\sqrt{2}$,点B在双曲线y=$\frac{k}{x}$上,点A在直线y=x上,则k的值为( )| A. | 1+$\frac{{\sqrt{2}}}{2}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | 2$\sqrt{2}$ |
 试判断如图所示的两个矩形是否相似.
试判断如图所示的两个矩形是否相似. 已知如图,E、F是AB上的两点,AE=BF,AC∥BD,且AC=DB,求证:(1)CF=DE.(2)CF∥DE.
已知如图,E、F是AB上的两点,AE=BF,AC∥BD,且AC=DB,求证:(1)CF=DE.(2)CF∥DE.