题目内容
1．
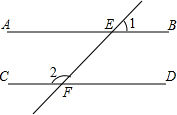如图，AB∥CD，直线EF分别交直线AB，CD于点E，F．若∠1=46°30′，则∠2的度数为（ ）| A． | 43°30′ | B． | 53°30′ | C． | 133°30′ | D． | 153°30′ |
分析 先根据平行线的性质求出∠EFD的度数，再根据补角的定义即可得出结论．
解答 解：∵AB∥CD，∠1=46°30′，
∴∠EFD=∠1=46°30′，
∴∠2=180°-46°30′=133°30′．
故选C．
点评 本题考查的是平行线的性质，用到的知识点为：两线平行，同位角相等．
练习册系列答案
相关题目
11．
某几何体的三视图如图所示，则这个几何体是（ ）
某几何体的三视图如图所示，则这个几何体是（ ）| A． | 球 | B． | 圆柱 | C． | 圆锥 | D． | 三棱柱 |
12．
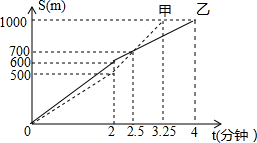甲、乙两人在操场上赛跑，他们赛跑的路程S（米）与时间t（分钟）之间的函数关系如图所示，则下列说法错误的是（ ）
甲、乙两人在操场上赛跑，他们赛跑的路程S（米）与时间t（分钟）之间的函数关系如图所示，则下列说法错误的是（ ）| A． | 甲、乙两人进行1000米赛跑 | |
| B． | 甲先慢后快，乙先快后慢 | |
| C． | 比赛到2分钟时，甲、乙两人跑过的路程相等 | |
| D． | 甲先到达终点 |
9．关于反比例函数y=-$\frac{2}{x}$，下列说法正确的是（ ）
| A． | 图象过（1，2）点 | B． | 图象在第一、三象限 | ||
| C． | 当x＞0时，y随x的增大而减小 | D． | 当x＜0时，y随x的增大而增大 |
6．下列关于二次函数y=ax2-2ax+1（a＞1）的图象与x轴交点的判断，正确的是（ ）
| A． | 没有交点 | B． | 只有一个交点，且它位于y轴右侧 | ||
| C． | 有两个交点，且它们均位于y轴左侧 | D． | 有两个交点，且它们均位于y轴右侧 |
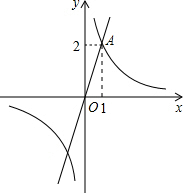如图，已知点A（1，2）是正比例函数y1=kx（k≠0）与反比例函数y2=$\frac{m}{x}$（m≠0）的一个交点．