题目内容
16.学生对小区居民的健身方式进行调查,并将调查结果绘制成如图两幅不完整的统计图.
请根据所给信息解答下列问题:
(1)本次共调查50人;
(2)补全图(1)中的条形统计图,图(2)中“跑步”所在扇形对应的圆心角度数是36°;
(3)估计2000人中喜欢打太极的大约有多少人?
分析 (1)用广场舞的人数除以广场舞所占的百分比,即可得到调查的人数;
(2)算出球类的人数,即可补全条形统计图;算出跑步所占的百分比乘以360°,即可得到所对应圆心角的度数;
(3)根据样本估计总体,即可解答.
解答 解:(1)18÷36%=50(人).
故答案为:50;
(2)球类的人数:50-3-17-18-5=7(人),“跑步”所在扇形对应的圆心角度数是:$\frac{5}{50}×36{0}^{°}$=36°,故答案为:36°;
如图所示:
(3)2000×$\frac{3}{50}$=120(人).
答:估计2000人中喜欢打太极的大约有120人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
11.近十天每天平均气温(℃)统计如下:24,23,22,24,24,27,30,31,30,29.关于这10个数据下列说法不正确的是( )
| A. | 众数是24 | B. | 中位数是26 | C. | 平均数是26.4 | D. | 极差是9 |
1.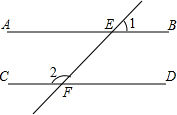 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为( )
 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F.若∠1=46°30′,则∠2的度数为( )| A. | 43°30′ | B. | 53°30′ | C. | 133°30′ | D. | 153°30′ |
5.方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
 如图是由5个完全相同的小正方体组成的几何体.则这个几何体的主视图是( )
如图是由5个完全相同的小正方体组成的几何体.则这个几何体的主视图是( )



 如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.
如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.