题目内容
2.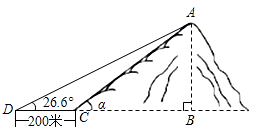 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )| A. | 164m | B. | 178m | C. | 200m | D. | 1618m |
分析 首先在直角三角形ABC中根据坡角的正切值用AB表示出BC,然后在直角三角形DBA中用BA表示出BD,根据BD与BC之间的关系列出方程求解即可.
解答 解:∵在直角三角形ABC中,$\frac{AB}{BC}$=tanα=1,
∴BC=AB,
∵在直角三角形ADB中,
∴$\frac{AB}{BD}$=tan26.6°=0.50,
即:BD=2AB,
∵BD-BC=CD=200,
∴2AB-AB=200,
解得:AB=200米,
答:小山岗的高度为200米;
故选C.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并求解.

练习册系列答案
相关题目
13.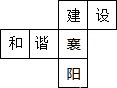 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )
一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )
 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )
一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面的字是( )| A. | 和 | B. | 谐 | C. | 襄 | D. | 阳 |
17.将抛物线y=-3x2-1向右平移1个单位长度,再向上平移1个单位长度后所得的抛物线的解析式为( )
| A. | y=-3(x-1)2 | B. | y=-3(x+1)2 | C. | y=-3(x-1)2+2 | D. | y=-3(x-1)2-2 |
14.实数a,b互为相反数,则下列结论正确的是( )
| A. | a+b=0 | B. | ab=1 | C. | a÷b=-l | D. | a>0,b<0 |
11.$\sqrt{64}$的算术平方根是( )
| A. | 8 | B. | ±8 | C. | $2\sqrt{2}$ | D. | ±$2\sqrt{2}$ |
12.说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 含30°的直角三角形 | D. | 顶角为45°的等腰三角形 |

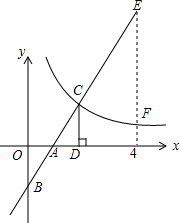 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: