题目内容
7.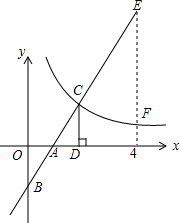 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对于直线解析式,分别令x与y为0求出y与x的值,确定出A与B坐标,利用AAS得到三角形OBA与三角形CDA全等,利用全等三角形对应边相等得到CD=OB,确定出C坐标,代入反比例解析式求出k的值,确定出反比例解析式,由图象判断y1<y2时x的范围,以及y1与y2的增减性,把x=2分别代入直线与反比例解析式,相减求出EF的长,即可做出判断.
解答 解:对于直线y1=2x-2,
令x=0,得到y=2;令y=0,得到x=1,
∴A(1,0),B(0,-2),即OA=1,OB=2,
在△OBA和△CDA中,$\left\{\begin{array}{l}{∠AOB=∠ADC=90°}\\{∠OAB=∠DAC}\\{OA=AD}\end{array}\right.$,
∴△OBA≌△CDA(AAS),
∴CD=OB=2,OA=AD=1,
∴C(2,2),
当x>0时,y1随x的增大而增大,y2随x的增大而减小;故①正确;
把C坐标代入反比例解析式得:k=4,故②正确;
由函数图象得:当0<x<2时,y1<y2,选项③正确;
当x=4时,y1=6,y2=1,即EF=6-1=5,选项④错误;
故选C
点评 此题考查了反比例函数与一次函数的交点,涉及的知识有:一次函数与坐标系的交点,待定系数法确定反比例函数解析式,坐标与图形性质以及反比例函数的性质,熟练掌握函数的性质是解本题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18.已知点P(-2,1)关于y轴的对称点为Q(m,n),则m-n的值是( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
2.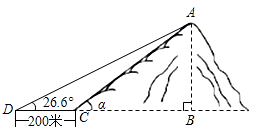 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )| A. | 164m | B. | 178m | C. | 200m | D. | 1618m |
12.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15分钟的频率是( )
| 通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 16 | 9 | 5 |
| A. | 0.1 | B. | 0.4 | C. | 0.5 | D. | 0.9 |
19.在实数-2,-1,0,2中,绝对值最小的实数是( )
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
16.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
根据表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
| 人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次测试成绩的众数是55分 | |
| C. | 该班学生这次测试成绩的中位数是60分 | |
| D. | 该班学生这次测试成绩的平均数是59分 |
 在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠:分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF对对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=1,则矩形纸片ABCD的周长为62.
在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠:分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF对对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=1,则矩形纸片ABCD的周长为62.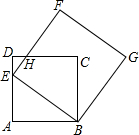 如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.
如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.