题目内容
20．绝对值是2的有理数是±2；数轴上A点表示的数是-2，那么同一数轴上与A点相距3个单位的点表示的数是-5或1．分析 根据绝对值的意义得到±2的绝对值为2，设同一数轴上与A点相距3个单位的点表示的数是x，再根据数轴上两点间的距离公式求出x的值即可．
解答 解：绝对值是2的有理数为±2．
设同一数轴上与A点相距3个单位的点表示的数是x，则|x+2|=3，解得x=1或x=-5．
故答案为±2，1或-5．
点评 本题考查的是数轴，绝对值：当a＞0时，|a|=a；当a=0时，|a|0；当a＜0时，|a|=-a，熟知数轴上两点间的距离公式是解答此题的关键．
练习册系列答案
相关题目
如图，等边△ABC的边长为4，AD是BC边上的中线，M是AD上的动点，E是AC边上的中点，则（EM+CM）2的最小值为（ ）
11．
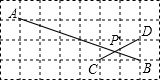如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD交于点P，则tan∠APC的值是（ ）
如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD交于点P，则tan∠APC的值是（ ）| A． | $\frac{2}{3}$ | B． | 1 | C． | 2 | D． | $\frac{\sqrt{3}}{2}$ |
8．
如图，在直角三角形ABC中，∠BAC=90°，AB=3，AC=4，将△ABC沿直线BC向右平移2.5个单位长度得到△DEF，连接AD，AE，则下列结论中不成立的是（ ）
如图，在直角三角形ABC中，∠BAC=90°，AB=3，AC=4，将△ABC沿直线BC向右平移2.5个单位长度得到△DEF，连接AD，AE，则下列结论中不成立的是（ ）| A． | AD∥BE，AD=BE | B． | ∠ABE=∠DEF | C． | ED⊥AC | D． | AE=DE=AD |
12．下列能判定△ABC为等腰三角形的是（ ）
| A． | ∠A=50°，∠B=40° | B． | ∠A=70°，∠B=40° | ||
| C． | AB=AC=4，BC=8 | D． | AB=3，BC=8，周长为16 |