题目内容
17.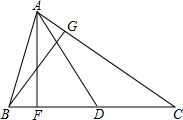 如图,△ABC的边BC上的高为AF,AC边上的高为BG,中线为AD,已知AF=6,BC=10,BG=5.
如图,△ABC的边BC上的高为AF,AC边上的高为BG,中线为AD,已知AF=6,BC=10,BG=5.(1)求△ABC的面积;
(2)求AC的长;
(3)试说明△ABD和△ACD的面积相等.
分析 (1)直接利用三角形的面积计算方法计算得出答案即可;
(2)利用三角形的面积计算公式建立方程求得答案即可;
(3)利用三角形的面积计算公式以及两个三角形底和高的关系得出答案即可.
解答 解:(1)∵△ABC的边BC上的高为AF,AF=6,BC=10,
∴△ABC的面积=$\frac{1}{2}$BC•AF=$\frac{1}{2}$×10×6=30;
(2)∵AC边上的高为BG,BG=5,
∴△ABC的面积=$\frac{1}{2}$AC•BG=30,
∴AC=12;
(3)∵△ABC的中线为AD,
∴BD=CD,
∵△ABD以BD为底,△ACD以CD为底,而且等高,
∴S△ABD=S△ACD.
点评 此题考查三角形的面积计算公式,掌握三角形的面积=$\frac{1}{2}$×底×高是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.根据阿里巴巴公布的实时数据,截至2016年11月11日24时,天猫双11全球狂欢节总交易额约1207亿,把这个数据用科学记数法表示为( )
| A. | 1207×108元 | B. | 12.07×1010元 | C. | 1.207×108元 | D. | 1.207×1011元 |
9.下列分数中不能化为有限小数的是( )
| A. | $\frac{7}{25}$ | B. | $\frac{7}{32}$ | C. | $\frac{3}{80}$ | D. | $\frac{5}{6}$ |
6.2016年10月17日,神州十一号载人飞船上天,到达距离地面393公里轨道的新高度,我国开始实施航天员中期驻留试验,目前在轨飞行速度约为7820米/秒,其中数据7820用科学记数法表示为( )
| A. | 7.8×103 | B. | 78.2×102 | C. | 7.82×103 | D. | 7.82×104 |
12.据工信部发布的2015年通信运营业统计公报显示,2015年,全国电话用户总数达到15.37亿户,其中移动电话用户总数达13.06亿户,13.06亿科学记数法可表示为( )
| A. | 13.06×108 | B. | 1.306×108 | C. | 1.306×109 | D. | 13.06×109 |
6.若y=$\frac{9}{2}$,则$\frac{2x+6}{12y}$÷$\frac{x+3}{12{y}^{2}}$的结果为( )
| A. | 6 | B. | 9 | C. | $\frac{9}{2}$ | D. | $\frac{81}{4}$ |
6.已知地球上海洋面积约为361000000km2,361000000用科学记数法可以表示为( )
| A. | 36.1×107 | B. | 3.61×107 | C. | 3.61×108 | D. | 3.61×109 |

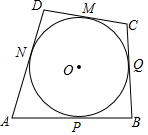 己知四边形ABCD的边AB、BC、CD、DA分别与⊙O相切于P、Q、M、N,探究四边形四边有何特点.
己知四边形ABCD的边AB、BC、CD、DA分别与⊙O相切于P、Q、M、N,探究四边形四边有何特点.