题目内容
12.已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.分析 延长AB到F,使BF=BD,连DF,首先证明△ADF≌△ADC,推出AF=AC,由BE是角平分线,推出∠CBE=$\frac{1}{2}$∠ABC=40°推出∠EBD=∠C,推出BE=EC,推出BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.
解答 证明:延长AB到F,使BF=BD,连DF,
∴∠F=∠BDF,
∵∠A:∠B:∠C=3:4:2,
∴∠ABC=80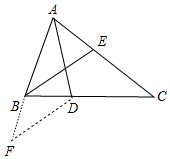 °,∠ACB=40°,
°,∠ACB=40°,
∴∠F=40°,∠F=∠ACB,
∵AD是平分线,
∴∠BAD=∠CAD,
在△ADF和△ADC中,
$\left\{\begin{array}{l}{AD=AD}\\{∠DAF=∠DAC}\\{∠F=∠C}\end{array}\right.$,
∴△ADF≌△ADC,
∴AF=AC,
∵BE是角平分线,
∴∠CBE=$\frac{1}{2}$∠ABC=40°
∴∠EBD=∠C,
∴BE=EC,
∴BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.
∴AB+BD=AE+BE.
点评 本题考查全等三角形的判定和性质、角平分线的性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.在△ABC中,点D,E分别在边AB,AC上,$\frac{AD}{BD}$=$\frac{1}{2}$,要使DE∥BC,还需满足下列条件中的( )
| A. | $\frac{DE}{BC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{3}$ | C. | $\frac{AE}{AC}$=$\frac{1}{2}$ | D. | $\frac{AE}{AC}$=$\frac{1}{3}$ |
1.下列说法正确的是( )
| A. | 有理数包括正数、零和负数 | |
| B. | -a2一定是负数 | |
| C. | 34.37°=34°22′12″ | |
| D. | 两个有理数的和一定大于每一个加数 |
 如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.
如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.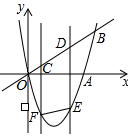 如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.
如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.