题目内容
4. 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
分析 根据等腰直角三角形的性质得出BC的长,再利用tan70.5°=$\frac{AC}{BC}$求出答案.
解答 解:∵在Rt△DBC中,∠DBC=45°,且CD=2.3米,
∴BC=2.3m,
∵在Rt△ABC中,∠ABC=70.5°,
∴tan70.5°=$\frac{AC}{BC}$=$\frac{AD+2.3}{2.3}$≈2.824,
解得:AD≈4.2,
答:像体AD的高度约为4.2m.
点评 此题主要考查了解直角三角形的应用,正确掌握锐角三角函数关系是解题关键.

练习册系列答案
相关题目
14.某地组织20辆汽车装运A,B,C三种苹果42吨到外地销售.按规定每辆车只装一种苹果,且必须装满,每种苹果不少于2车.
(1)设用x辆车装运A种苹果,用y辆车装运B种苹果.根据上表提供的信息,求y与x之间的函数关系式,并求出x的取值范围;
(2)设此次外销活动的利润为W(百元),求W与x之间的函数关系式,x为何值时W(百元)取得最大利润,并安排此时相应的车辆调配方案.
| 苹果品种 | A | B | C |
| 每辆汽车(吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利(百元) | 6 | 8 | 5 |
(2)设此次外销活动的利润为W(百元),求W与x之间的函数关系式,x为何值时W(百元)取得最大利润,并安排此时相应的车辆调配方案.
15.已知正比例函数y=(-2k+2)x,若y随x的增大而增大,则k的取值范围是( )
| A. | k≤1 | B. | k≥1 | C. | k<1 | D. | k>1 |
9.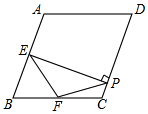 如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
 如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 45° |
16.几个相同的小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置小正方体的个数最多是( )
俯视图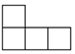 左视图
左视图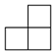
俯视图
 左视图
左视图
| A. | 5个 | B. | 7个 | C. | 8个 | D. | 9个 |
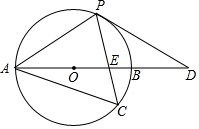 如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.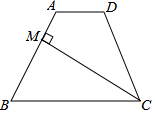 如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1.
如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1. 已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.
已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.