题目内容
15. 如图,过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.
如图,过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.
分析 首先连接AC,PC,由四边形ABCD是正方形,可得BD垂直平分AC,即可证得AP=PC,又由PE⊥BC,PF⊥CD,证得四边形PECF是矩形,可判定EF=PC,继而证得结论.
解答 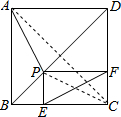 证明:连接AC,PC,
证明:连接AC,PC,
∵四边形ABCD是正方形,
∴BD垂直平分AC,∠BCD=90°,
∴AP=CP,
∵PE⊥BC,PF⊥CD,
∴∠PEC=∠PFC=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴AP=EF.
点评 此题考查了正方形的性质、矩形的判定与性质以及线段垂直平分线的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
10.弹簧挂上物体后会伸长,现测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)之间有如下关系:
下列说法不正确的是( )
| 物体质量x/千克 0 1 2 3 4 5… |
| 弹簧长度y/厘米 10 10.5 11 11.5 12 12.5… |
| A. | x与y都是变量,其中x是自变量,y是因变量 | |
| B. | 弹簧不挂重物时的长度为0厘米 | |
| C. | 在弹簧范围内,所挂物体质量为7千克时,弹簧长度为13.5厘米 | |
| D. | 在弹簧范围内,所挂物体质量每增加1千克弹簧长度增加0.5厘米 |
 如图1、图2都是由8个一样的小长方形拼(围)成的大矩形,且图2中的明影部分(小矩形)的面积为1cm2.则小长方形的长为( )
如图1、图2都是由8个一样的小长方形拼(围)成的大矩形,且图2中的明影部分(小矩形)的面积为1cm2.则小长方形的长为( )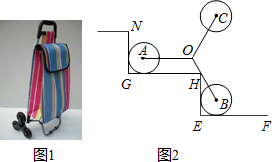 如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是$\sqrt{3}$.
如图所示是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是$\sqrt{3}$.