题目内容
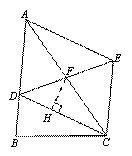
如图,在△ABC中,D为AB边上一点、F为AC的中点,过点C作CE//AB交DF的延长线于点E,连结AE.
(1)求证:四边形ADCE为平行四边形.
(2)若EF=2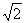 ,
,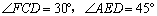 ,求DC的长.
,求DC的长.
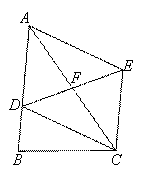
(1)证明:∵CE//AB,∴∠DAF=∠ECF.
∵F为AC的中点,∴AF=CF.
在△DAF和△ECF中
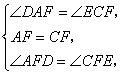
∴ △DAF≌△ECF.
∴ AD=CE.
∵CE//AB,
∴ 四边形ADCE为平行四边形. (2)作FH⊥DC于点H.
 ∵ 四边形ADCE为平行四边形.
∵ 四边形ADCE为平行四边形.
∴ AE//DC,DF= EF=2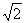 , ∴∠FDC =∠AED=45°.
, ∴∠FDC =∠AED=45°.
在Rt△DFH中,∠DHF=90°,DF=2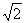 ,∠FDC=45°,
,∠FDC=45°,
∴ sin∠FDC=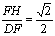 ,得FH=2,
,得FH=2,
tan∠FDC= ,得DH=2.
,得DH=2.
在Rt△CFH中,∠FHC=90°,FH=2,∠FCD=30°,∴ FC=4.
由勾股定理,得HC=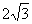 .
.
∴ DC=DH+HC=2+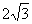 .
.

练习册系列答案
相关题目
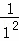 +
+ ,S2=1+
,S2=1+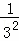 ,S3=1+
,S3=1+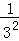 +
+ …Sn=1+
…Sn=1+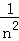 +
+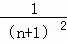
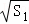 = ,
= , = ;猜想
= ;猜想 = (用n的代数式表示);
= (用n的代数式表示);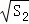 +
+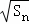 (用n的代数式表示).
(用n的代数式表示). .
.
 B C D
B C D
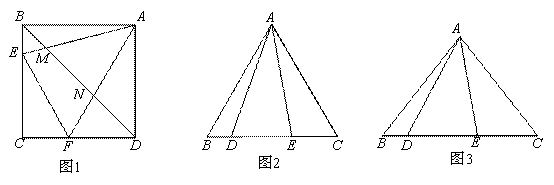
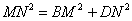 ,请证明这个等量关系;
,请证明这个等量关系;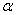 ,(0°<
,(0°<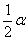 时,BD、DE、EC应满足的等量关系是____________________.【参考:
时,BD、DE、EC应满足的等量关系是____________________.【参考: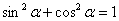 】
】
 ,则
,则 的度数是
的度数是
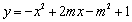 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C. 是等腰三角形,求抛物线的解析式;
是等腰三角形,求抛物线的解析式; ,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线
,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线 时,点M位于点N的下方,求这个一次函数的解析式.
时,点M位于点N的下方,求这个一次函数的解析式.
 的整数解
的整数解