题目内容
已知抛物线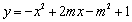 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
(1)试用含m的代数式表示A、B两点的坐标;
(2)当点B在原点的右侧,点C在原点的下方时,若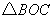 是等腰三角形,求抛物线的解析式;
是等腰三角形,求抛物线的解析式;
(3)已知一次函数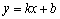 ,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线
,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线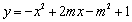 于点N,若只有当
于点N,若只有当 时,点M位于点N的下方,求这个一次函数的解析式.
时,点M位于点N的下方,求这个一次函数的解析式.
解:(1)令 ,有
,有 .
.
∴ . ∴
. ∴ .
.
∴ ,
, .
.
∵点B在点A的右侧,
∴ ,
, .
.
(2)∵点B在原点的右侧且在点A的右侧,点C在原点的下方,抛物线开口向下,
∴ .∴
.∴ .
.
∴ .
.
令 ,有
,有 .
.
∴ .
.
∵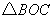 是等腰三角形,且∠BOC =90°,
是等腰三角形,且∠BOC =90°,
∴ .即
.即 .
.
∴ .
.
∴ ,
, (舍去).
(舍去).
∴ .
.
∴抛物线的解析式为 .
.
(3)依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为1和4,
由此可得交点坐标为 和
和 .
.
将交点坐标分别代入一次函数解析式 中,
中,
得 解得
解得 
一次函数的解析式为 .
.

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.
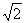 ,
,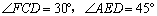 ,求DC的长.
,求DC的长.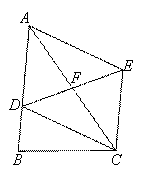
 B C D
B C D 有两个不相等的实数根,则a的取值范围是_________.
有两个不相等的实数根,则a的取值范围是_________. B.
B.  C.
C.  D.
D. 