题目内容
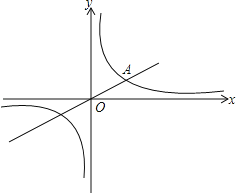
【题目】已知一次函数y=![]() x﹣2的图象经过(a,b),(a+1,b+k)两点,并且与反比例函数
x﹣2的图象经过(a,b),(a+1,b+k)两点,并且与反比例函数![]() 的图象交于第一象限内一点A.
的图象交于第一象限内一点A.
(1)求反比例函数的解析式;
(2)请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)存在.P1(﹣2,0),P2(2,0),P3(2
;(2)存在.P1(﹣2,0),P2(2,0),P3(2![]() ,0),P4(
,0),P4(![]() ,0).
,0).
【解析】
(1)由一次函数y=![]() x﹣2的图象经过(a,b),(a+1,b+k)两点,即可得到方程组
x﹣2的图象经过(a,b),(a+1,b+k)两点,即可得到方程组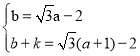 ,解此方程组,即可求得k的值,从而求出反比例函数的解析式;
,解此方程组,即可求得k的值,从而求出反比例函数的解析式;
(2)联立一次函数与反比例函数的解析式,得 ,解此方程组,即可求得点A的坐标;分别从OP=OA,OA=PA,AP=AP去分析求解,结合图形,即可求得符合条件的点P的坐标
,解此方程组,即可求得点A的坐标;分别从OP=OA,OA=PA,AP=AP去分析求解,结合图形,即可求得符合条件的点P的坐标
(1)∵一次函数y=![]() x﹣2的图象经过(a,b),(a+1,b+k)两点,
x﹣2的图象经过(a,b),(a+1,b+k)两点,
∴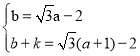 ,
,
②﹣①得:k=![]() ,
,
∴反比例函数的解析式为:y=![]() ;
;
(2)存在.
联立一次函数与反比例函数的解析式,得: ,
,
解得: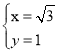 或
或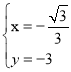 ,
,
∵点A在第一象限内,
∴点A的坐标为(![]() ,1);
,1);
过点A作AB⊥x轴于B,
∵点A(![]() ,1),
,1),
∴OA=![]() =2,
=2,
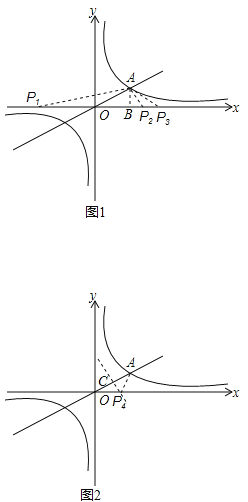
如图1:当OP=OA时,OP=2,
则P1(﹣2,0),P2(2,0);
当OA=PA时,OB=BP=![]() ,
,
∴OP=OB+BP=2![]() ,
,
∴P3(2![]() ,0);
,0);
如图2:取OA的中点C,过点C作PC⊥OA,交x轴于P,
则OP=AP,
∵OA=2,
∴OC=![]() OA=1,
OA=1,
∵∠AOP=30°,
∴OP=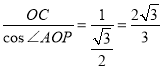 ,
,
∴P4(![]() ,0).
,0).
综上,符合条件的点P的坐标为:P1(﹣2,0),P2(2,0),P3(2![]() ,0),P4(
,0),P4(![]() ,0).
,0).

【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5