Question

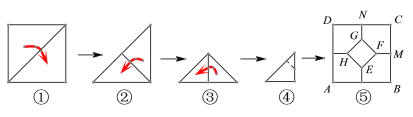
【题目】将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM、GN是折痕，若正方形EFGH与五边形MCNGF面积相等，则的值是____________

Answer 1

【答案】

【解析】

连接HF，设直线MH与AD边的交点为P，根据剪纸的过程以及折叠的性质得PH=MF且正方形EFGH的面积=×正方形ABCD的面积，从而用a分别表示出线段GF和线段MF的长即可求解．

连接HF，设直线MH与AD边的交点为P，如图：

由折叠可知点P、H、F、M四点共线，且PH=MF，设正方形ABCD的边长为2a，则正方形ABCD的面积为4a2，
∵若正方形EFGH与五边形MCNGF的面积相等
∴由折叠可知正方形EFGH的面积=×正方形ABCD的面积=，
∴正方形EFGH的边长GF==，

∴HF=，

∴MF=PH=，

∴=.