题目内容
【题目】问题探究：已知平行四边形
的面积为
，
是
所在直线上一点．
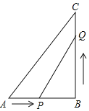
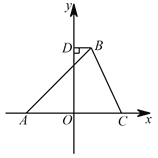
如图
：当点与
重合时，
________；
如图
，当点与与
均不重合时，________；
如图
，当点在（或
）的延长线时，________．
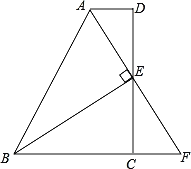
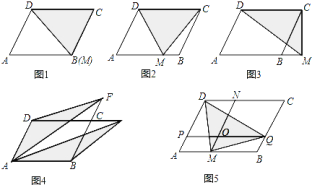
拓展推广：如图
，平行四边形的面积为
，
、
分别为
、
延长线上两点，连接
、
、
、
，求出图中阴影部分的面积，并说明理由．
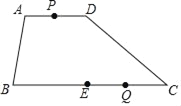
实践应用：如图是一平行四边形绿地，
、
分别平行于、
，它们相交于点
，
，
，
，
，现进行绿地改造，在绿地内部作一个三角形区域
（连接
、
、
，图中阴影部分）种植不同的花草，求出三角形区域的面积．
【答案】（1）
；（2）；（3）；拓展推广：阴影部分的面积
；实践应用：三角形区域的面积
．
【解析】
(1)平行四边形的面积等于底乘以高，设平行四边形ABCD的高为h， △DCM边CD的高也为h，由题S平行四边形ABCD=CD×h，S△DCM=
CD×h=S平行四边形ABCD=50；
(2)由（1）同理可得S△DCM =50；
(3)由（1）同理可得S△DCM =50；
拓展推广：由（1）的结论可得S△ADF=a， S△ABE=a，由此即可得阴影部分的面积；
应用，由推广的结论，有
，
，
，由此即可求出三角形区域的面积.
设平行四边形ABCD的边CD上的高为h，则△DCM边CD的高也为h，
∵S平行四边形ABCD=CD×h，则平行四边形
的面积
，
；
与同理可得
；
与同理可得；
拓展推广：
根据
的结论，
，
，
∴阴影部分的面积
；
实践应用：
根据前面信息，
，
，
，
∴三角形区域的面积
．
练习册系列答案
相关题目
