题目内容
4.在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E. 将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.(1)求证:△ABE≌△CDF;
(2)求证:四边形BFDE为平行四边形;
(3)若四边形BFDE为菱形,且AB=2,求BC的长.
分析 (1)根据矩形和翻折的性质可知,∠A=∠C,AB=CD,∠ABE=∠CDF.即可证△ABE≌△CDF;
(2)由△ABE≌△CDF,推出AE=CF,求出DE=BF,DE∥BF,根据平行四边形判定推出即可;
(3)求出∠ABE=30°,根据直角三角形性质求出AE、BE,即可求出答案.
解答 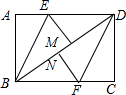 (1)证明:如图,∵四边形ABCD是矩形,
(1)证明:如图,∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD.
∴∠ABD=∠CDB.
∵在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,
∴∠ABE=∠EBD=$\frac{1}{2}$∠ABD,∠CDF=$\frac{1}{2}$∠CDB.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CD}\\{∠ABE=∠CDF}\end{array}\right.$,
∴△ABE≌△CDF(ASA).
(2)证明;∵△ABE≌△CDF,
∴AE=CF.
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC.
∴DE=BF,DE∥BF.
∴四边形BFDE为平行四边形.
(3)解:∵四边形BFDE为为菱形,
∴EF⊥BD,
∵EM⊥BD,FN⊥BD,
∴M,N两点重合.
∴BD=2BM=4,
在Rt△BDC中,
BC=2$\sqrt{3}$.
点评 本题考查了平行四边形的判定,菱形的性质,矩形的性质,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
相关题目
13.在等腰三角形、平行四边形、直角梯形和圆中,既是轴对称图形又是中心对称图形的是( )
| A. | 等腰三角形 | B. | 平行四边形 | C. | 直角梯形 | D. | 圆 |
15.若代数式2x2+3x-3的值为11,则代数式6x2+9x+2013的值为( )
| A. | 2002 | B. | 2013 | C. | 2024 | D. | 2055 |
19.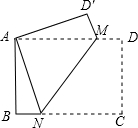 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )| A. | 1:3 | B. | 1:4 | C. | 1:6 | D. | 1:9 |
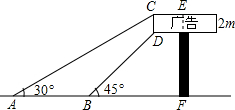 如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)
如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号) 如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处
如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处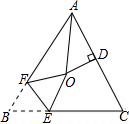 如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.
如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.