题目内容
2.已知(a4bn+2)(a2n-1b2m)=am+2bn,求m+n的值.分析 根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可.
解答 解:(a4bn+2)(a2n-1b2m)=a2n+3bn+2+2m=am+2bn,得
$\left\{\begin{array}{l}{2n+3=m+2}\\{n+2+2m=n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=-1}\end{array}\right.$,
m+n=-1+(-1)=-2.
点评 本题考查了单项式与单项式相乘,熟练掌握运算法则是解题的关键.

练习册系列答案
相关题目
13.下列说法中,正确的是( )
| A. | x=5是方程x+5=0的解 | B. | y=5是3y+15=0的解 | ||
| C. | z=-1是-$\frac{z}{4}$=4的解 | D. | x=0.04是方程25x=1的解 |
9.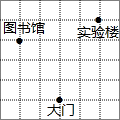 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )| A. | (1,5) | B. | (-2,3) | C. | (-2,-1) | D. | (-2,1) |
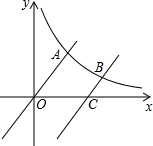 如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.
如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.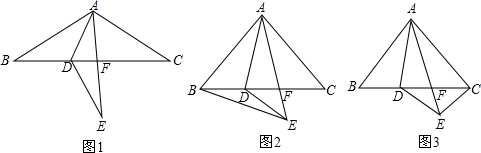
 如图,已知四边形ABCD以及点O.
如图,已知四边形ABCD以及点O.