题目内容
6.若二次函数y=ax2+bx,当x取x1,x2(x1≠x2)时,函数值相等,则x取x1+x2时,函数的值为0.分析 由于ax12+bx1=ax22+bx2,移项后分解得到(x1-x2)(ax1+ax2+b)=0,而x1≠x2,所以ax1+ax2+b=0,即x1+x2=-$\frac{b}{a}$,然后把x=-$\frac{b}{a}$代入二次函数解析式中计算即可.
解答 0解:根据题意得ax12+bx1=ax22+bx2,
ax12-ax22+bx1-bx2=0,
a(x1-x2)(x1+x2)+b(x1-x2)=0,
(x1-x2)(ax1+ax2+b)=0,
∵x1≠x2,
∴ax1+ax2+b=0,即x1+x2=-$\frac{b}{a}$,
∴当x=x1+x2=-$\frac{b}{a}$时,y=a×(-$\frac{b}{a}$)2+b×(-$\frac{b}{a}$)=0.
故答案为0.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,当x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;当x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

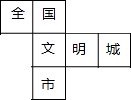 在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )
在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )| A. | 全 | B. | 国 | C. | 明 | D. | 城 |
| A. | x2+2x=x2-1 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=2(x+1) |
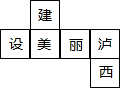 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 泸 | D. | 西 |
| A. | 正方形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
 △ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.
△ABC中,AB=AC,AD⊥BC,∠BAC=∠ACG=4∠EDC,CG=AD=4,$\frac{{{S_{△DEC}}}}{{{S_{△ACG}}}}$=$\frac{1}{4}$,BC=4$\sqrt{5}$.